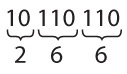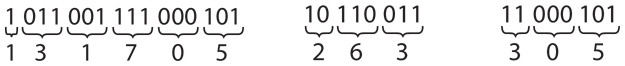
В главе 8 эта техника описана подробно. Тем не менее для преобразования двоичных чисел в десятичные и обратно обычно требуется бумага, карандаш и практика.
Мы уже узнали о восьмеричной системе счисления — системе счисления с основанием 8, где используются только цифры 0, 1, 2, 3, 4, 5, 6 и 7. Преобразовать восьмеричное число в двоичное легко. Все, что нужно, — это запомнить 3-битный эквивалент каждой восьмеричной цифры.
Двоичное число
Восьмеричное число
000
0
001
1
010
2
011
3
100
4
101
5
110
6
111
7
Если у вас есть двоичное число (например, 10110110), начинайте преобразование с правого края. Каждая группа из трех бит соответствует восьмеричной цифре.
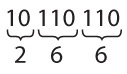
Таким образом, байт 10110110 можно выразить в виде восьмеричного числа 266. Это выражение, безусловно, является более лаконичным, значит, восьмеричная система действительно подходит для представления байтов. Однако у нее есть небольшой недостаток.
В двоичной системе байты выражаются значениями в диапазоне от 00000000 до 11111111, в восьмеричной — значениями в диапазоне от 000 до 377. Как было показано в предыдущем примере, средней и крайней справа восьмеричным цифрам соответствуют группы из трех бит, однако крайней слева восьмеричной цифре соответствуют только два бита. Это означает, что восьмеричное представление 16-разрядного числа не совпадает с восьмеричными представлениями двух байтов, составляющих это 16-разрядное число.
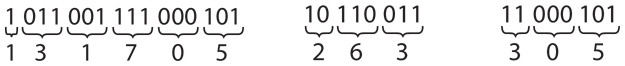
Чтобы согласовать представления многобайтных значений с представлениями отдельных байтов, нужна система, в которой каждый байт делится на равное количество битов. Следовательно, нам требуется разделить каждый байт на четыре значения по два бита каждое (система счисления с основанием 4) или на два значения по четыре бита каждое (система счисления с основанием 16).
Систему счисления с основанием 16 мы еще не рассматривали, и на то есть причины. Система счисления с основанием 16 называется шестнадцатеричной
[18], — даже название труднопроизносимо. В десятичной системе счисления считаем так:
0 1 2 3 4 5 6 7 8 9 10 11 12 …
В восьмеричной системе, как вы помните, не используются цифры 8 и 9:
0 1 2 3 4 5 6 7 10 11 12 …
В системе с основанием 4 не требуются цифры 4, 5, 6 и 7:
0 1 2 3 10 11 12 …
Наконец, в двоичной системе достаточно только 0 и 1:
0 1 10 11 100 …
Однако шестнадцатеричная система отличается тем, что в ней используется больше цифр, чем в десятичной. В шестнадцатеричной системе подсчет происходит примерно так:
0 1 2 3 4 5 6 7 8 9 ? ? ? ? ? ? 10 11 12 …
В данном случае 10 соответствует числу 16ДЕСЯТЬ. Вопросительные знаки говорят о том, что нам нужны еще шесть символов для представления шестнадцатеричных чисел. Что это за символы? Откуда их брать? Что ж, поскольку они не достались нам в наследство, подобно другим традиционным числовым символам, мы можем придумать их самостоятельно, например такие.

В отличие от символов, используемых для обозначения большинства чисел, у этих обозначений есть преимущество: они легко запоминаются и отождествляются с теми величинами, которые представляют. Существует так называемая десятигаллонная ковбойская шляпа, мяч для американского футбола (11 игроков в команде), дюжина пончиков (12 штук), черная кошка (с которой ассоциируется несчастливое число 13), полная луна (появляется на небе через 14 дней после новолуния) и кинжал (напоминающий об убийстве Юлия Цезаря в 15-й день марта). Каждый байт можно выразить в виде двух шестнадцатеричных цифр. Другими словами, шестнадцатеричная цифра эквивалентна четырем битам, или одной тетраде. В следующей таблице показаны соответствия двоичных, шестнадцатеричных и десятичных чисел.
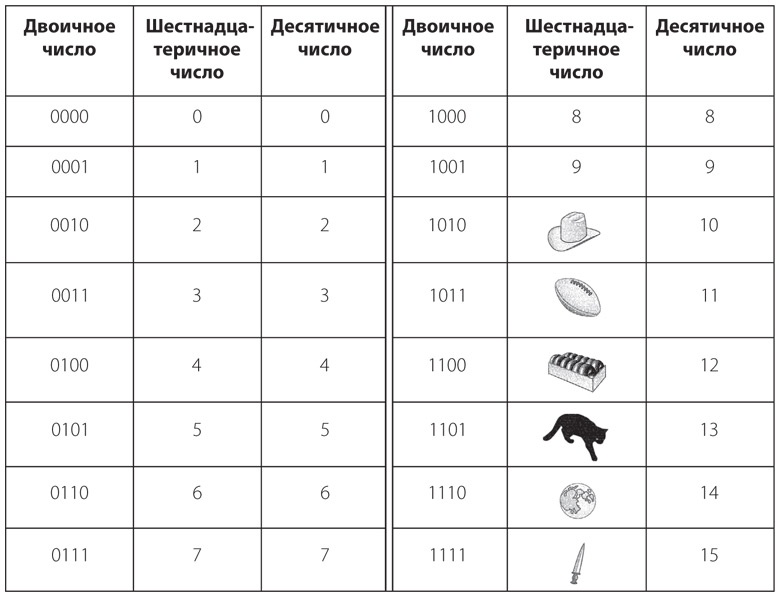
Вот как можно представить двоичное число 10110110 в шестнадцатеричной системе.
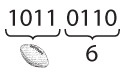
И не важно, имеем ли мы дело с многобайтными числами.
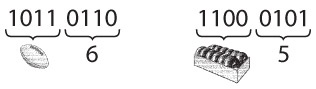
Один байт всегда представляется парой шестнадцатеричных цифр.
К сожалению (а может быть, к счастью), мы не собираемся использовать футбольные мячи и пончики для записи шестнадцатеричных чисел, хотя они, безусловно, могли бы сгодиться для этой цели. Вместо них в шестнадцатеричной системе применяются обозначения, приводящие многих в замешательство. Дело в том, что шесть недостающих шестнадцатеричных цифр представляют шестью первыми буквами латинского алфавита:
0 1 2 3 4 5 6 7 8 9 A B C D E F 10 11 12 …
В следующей таблице показано реальное соответствие между двоичными, шестнадцатеричными и десятичными числами.
Двоичное число
Шестнадцатеричное число
Десятичное число
0000
0
0
0001
1
1
0010
2
2
0011
3
3
0100
4
4
0101
5
5