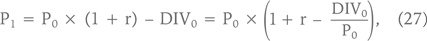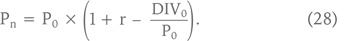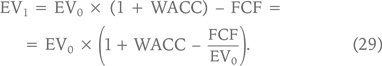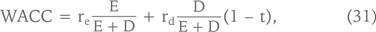Книга Как оценить бизнес по аналогии: Пособие по использованию сравнительных рыночных коэффициентов, страница 34. Автор книги Елена Чиркова

Онлайн книга «Как оценить бизнес по аналогии: Пособие по использованию сравнительных рыночных коэффициентов»

Страница

До сих пор мы конструировали мультипликаторы, основанные на будущих показателях компании, оперируя лишь знаменателем мультипликатора, между тем в числителе стояла текущая цена акций. А теперь я задам очень сложный вопрос, пожалуй, самый сложный в данной книге.

Такой пример постаралась придумать и я, но о нем речь пойдет чуть позже, а пока мы займемся тем, что введем новый вид мультипликаторов, у которых не только знаменатель, но и числитель являются оценками будущего. Сначала аналитики ввели ожидаемые оценки в числитель мультипликаторов вида «EV/…». Показатель EV, представляющий собой сумму цен акций и чистого долга, стали заменять на сумму вида MC0 + NDt, т. е. на сумму текущей капитализации и будущего чистого долга. Такая сумма является чисто умозрительной конструкцией, однако поправка на будущий долг позволила сделать более корректным сравнение компаний, у которых изменение чистого долга в прогнозном периоде будет демонстрировать разную динамику.

Затем появились мультипликаторы, в числителе которых использовались и будущие цены акций, поэтому мы будем называть их «мультипликаторами на основе форвардных цен» (forward priced, или forward looking multiples). Числитель таких мультипликаторов имеет вид: MCt + NDt.

Мы можем рассчитать цену акции в будущем периоде по следующей формуле:

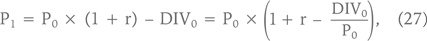
где r – как всегда, доходность, требуемая инвесторами на вложения в данную акцию, DIV – дивиденды, а DIV0/P0 – «доходность акции по дивидендам», или «дивидендная доходность» (dividend yield). Если r1 = r2 =… = rn и DIV0/P0 = DIV1/P1 =… = DIVn/Pn; то ^[68]

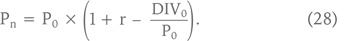
Аналогичным образом можно рассчитать и будущую стоимость компании – EV. Существуют два метода расчета будущей величины EV. Первый метод – прямой: по той же формуле, по которой рассчитывалась будущая стоимость акции. Отличие состоит в том, что при определении стоимости бизнеса (EV) доходность, требуемая инвесторами на вложения в акции, будет заменена в этой формуле на WACC – средневзвешенную стоимость капитала или средневзвешенную доходность для всех сторон, финансирующих компанию, а дивиденды, или денежные потоки акционеров, будут заменены на доходы всех провайдеров капитала, т. е. на свободный денежный поток, попавший в распоряжение акционеров и кредиторов (назовем его в нижеследующей формуле для краткости FCF (денежный поток акционеров и кредиторов – free cash flow)).

Тогда мы получим «аналог» формулы (27) для стоимости бизнеса:

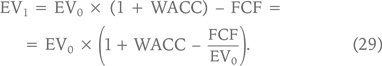
По аналогии с тем, как DIVt/Pt – 1 называют dividend yield, FCFt/EVt – 1 называют FCF yield, что можно попытаться перевести весьма громоздкой фразой «доходность бизнеса по денежному потоку (акционеров и кредиторов)».

Для случая, когда WACC = const и FCF yield = const, формула EVn выглядит следующим образом:

EVn = EV0 × (1 + WACC) – FCF yieldn. (30)

Напомним, что WACC рассчитывается по формуле:

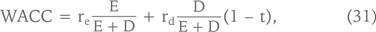
где E ^[69] – рыночная стоимость акционерного капитала;

re – требуемая доходность на акционерный капитал;

D – рыночная стоимость долга;

rd – процентная ставка по долгу;

t – ставка налога на прибыль;

rd × (1 – t) – посленалоговая (after tax) процентная ставка.

Второй метод – косвенный: тот же результат можно получить, прибавив к будущей рыночной капитализации будущий чистый долг, который, в свою очередь, будет рассчитываться из текущего чистого долга с учетом его изменений (выплаты процентов и изменения основной суммы долга) за требуемый период.

Страница