Перемещение любой типичной галактики во фридмановских моделях в точности повторяет движение брошенного вверх камня. Если его метнуть достаточно сильно или, что то же самое, если у Земли достаточно маленькая масса, камень будет постепенно замедляться, но в конце концов уйдет на бесконечность. Это соответствует случаю, когда плотность Вселенной меньше критической. Если же придать камню не очень большую скорость, то он, достигнув некоторой верхней точки, рухнет вниз. Это, разумеется, соответствует плотности Вселенной, большей, чем критическая.
Из этой аналогии, в общем-то, ясно, почему Эйнштейн не мог найти статическое решение своих уравнений: мы вполне привычны к зрелищу падающего или летящего вверх камня, но вот чтобы он надолго завис в воздухе… Эта аналогия, кстати, помогает рассеять и распространенное заблуждение по поводу расширения Вселенной. Галактики разбегаются не потому, что их растаскивает какая-то загадочная сила, – точно так же камень летит вверх не потому, что отталкивается Землей. Они удаляются друг от друга потому, что в прошлом их разметал некий взрыв.
По сути, с помощью этой аналогии можно подробно исследовать многие свойства фридмановских моделей, не прибегая к общей теории относительности, хотя в 1920-х гг. об этом еще не знали. Чтобы предсказать движение той или иной типичной галактики, нарисуйте сферу с наблюдателем в центре и радиусом, равным расстоянию от нас до этой галактики. Тогда последняя будет двигаться так, словно вся масса Вселенной сосредоточена в пределах этой сферы, а снаружи ничего нет. Посмотрим на это явление с другой стороны. Допустим, мы пробурили в земле скважину и бросаем туда различные тела. Тогда увидим, что измеряемое ускорение силы тяжести по направлению к центру земного шара будет определяться исключительно веществом, лежащим ниже нашей скважины (словно поверхность Земли проходит через ее дно). Это потрясающий результат можно сформулировать в виде теоремы, верной как в ньютоновской, так и в эйнштейновской теории гравитации. Ее единственное условие – сферическая симметрия исследуемой системы. Такую теорему в рамках общей теории относительности американский математик Дж. Д. Биркгоф доказал еще в 1923 г., однако значение этого для космологии было оценено лишь спустя десятилетия.
Так, лишь гораздо позже выяснилось, что с помощью теоремы Биркгофа можно рассчитать критическую плотность во фридмановских моделях (рис. 3). Если представить себе сферу с нами в центре и проходящую при этом через какую-нибудь далекую галактику, то, зная массу вещества внутри этой сферы, можно вычислить скорость убегания. (Скорость убегания – та, при которой галактика на поверхности сферы сможет уйти на бесконечность.) Она оказывается пропорциональна радиусу сферы: чем больше последний, тем больше массы в пределах сферы и тем большая скорость нужна для убегания на бесконечность. Однако в законе Хаббла говорится: действительная скорость галактики на поверхности этой сферы пропорциональна расстоянию до нас, т. е. тоже радиусу сферы. Таким образом, хотя скорость убегания и зависит от радиуса, из отношения скорости галактики к скорости убегания размер сферы выпадает. Причем это справедливо для всех галактик и не зависит от того, какую из них мы примем за центр сферы. Получается, значения постоянной Хаббла и плотности Вселенной определяют будущее всех галактик, движение которых подчиняется закону Хаббла. Если их скорости превосходят скорость убегания, галактики уходят на бесконечность. В противном случае в некоторый момент в будущем все они упадут на нас. Критическая плотность – это всего-навсего плотность, при которой скорость убегания сравнивается со скоростью, следующей из закона Хаббла. И зависеть она может только от постоянной Хаббла, квадрату которой пропорциональна (см. математическую заметку 2 на с. 234).
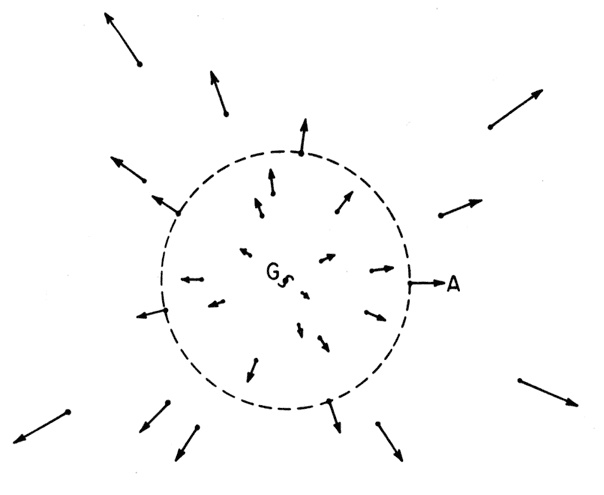
Рис. 3. Теорема Биркгофа и расширение Вселенной. Здесь изображены многочисленные галактики, а также их скорости по отношению к данной галактике G. Длина стрелок характеризует значения скоростей, которые, в соответствии с законом Хаббла, прямо пропорциональны расстоянию до G. Теорема Биркгофа утверждает: чтобы посчитать, как галактика A будет двигаться относительно G, достаточно учесть только ту массу, которая попадает в пределы сферы с центром в G, проходящей через A (на рисунке обозначена пунктиром). Если A расположена не слишком далеко от G, то гравитационное поле, создаваемое веществом в пределах сферы, будет умеренным. Это значит, что для расчета движения A можно применять рецепты ньютоновской механики
Выстраивая подобную логическую цепочку, можно более точно подсчитать зависимость размера Вселенной (другими словами, расстояния между любой парой типичных галактик) от времени (рис. 4). Но это приводит к уже несколько более сложным для понимания результатам. Есть, однако, один весьма простой факт, который нам позже пригодится. На ранних стадиях размер Вселенной менялся по простому степенному закону: если излучение ничтожно мало, размер пропорционален времени в степени 2/3, а когда плотность излучения превосходит плотность обычного вещества – в степени 1/2 (см. математическую заметку 3 на с. 237). Тем не менее одна из характерных черт моделей Фридмана не поддается объяснению, если не призвать на помощь общую теорию относительности. Речь идет о связи между плотностью и геометрией: Вселенная открыта и бесконечна или замкнута и конечна в зависимости от того, больше или меньше скорости галактик, чем скорость убегания.
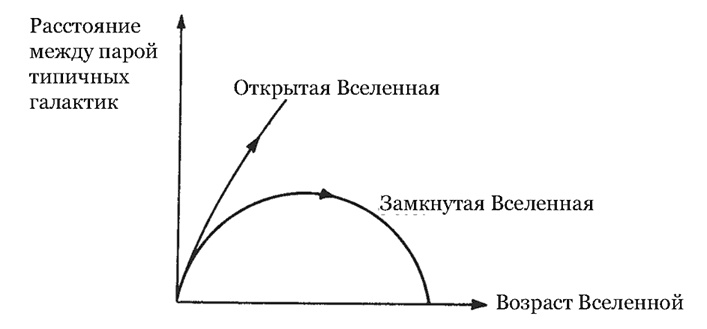
Рис. 4. Расширение и сжатие Вселенной. Изображенная здесь зависимость расстояния (в условных единицах) между парой типичных галактик от возраста Вселенной соответствует двум возможным космологическим моделям. В «открытом» случае мироздание бесконечно, плотность – меньше критической, а расширение хоть и замедляется, но будет продолжаться вечно. В «за мкнутом» случае Вселенная конечна, плотность – выше критической, а расширение однажды остановится и сменится сжатием. Приведенные графики рассчитаны с помощью эйнштейновских уравнений гравитационного поля без космологической постоянной и для материально-доминированной Вселенной
Один из способов узнать, превосходят галактические скорости скорость убегания или нет, – измерить, насколько интенсивно они уменьшаются со временем. Если это замедление меньше (или больше) определенного порога, то скорость галактик (не) превышает скорость убегания. С экспериментальной точки зрения это означает необходимость измерения кривизны графика зависимости красного смещения от расстояния до очень далеких галактик (рис. 5). Если постепенно переходить от плотной конечной Вселенной к менее плотной бесконечной, то участок графика, соответствующий большим расстояниям, будет постепенно выпрямляться. Построенная зависимость «красное смещение – расстояние», поведение которой нам больше всего интересно на далеких расстояниях, называется «диаграммой Хаббла».
Астрономы – сам Хаббл, Сэндидж и их последователи – потратили немало усилий, чтобы построить ее. Однако имеющиеся сегодня данные все еще не позволяют делать однозначные выводы. Проблема в том, что когда мы хотим узнать расстояние до очень далеких галактик, то, по понятным причинам, уже не можем полагаться на цефеиды или даже самые яркие звезды. Единственная величина, по которой можно оценить расстояние в этом случае, – видимая светимость самой галактики. Но откуда нам известно, что все наблюдаемые галактики имеют одинаковую абсолютную светимость? (Видимая светимость, напомним, – это лучистая энергия, приходящая на единицу площади нашего телескопа в единицу времени, а абсолютная – полная мощность, излучаемая астрономическим объектом во все стороны. Видимая светимость пропорциональна абсолютной и обратно пропорциональна квадрату расстояния.) Следует быть очень осторожным, дабы не пасть жертвой эффектов селекции – ведь чем дальше мы заглядываем, тем более яркие галактики будут попадаться нам на глаза. Еще одно, более серьезное препятствие – эволюция галактик. Рассматривая в телескопы очень далекие из них, мы видим их такими, какими они были миллиарды лет назад, когда принимаемый нами свет только-только покинул их. Если в ту эпоху галактики в большинстве своем были ярче, чем сейчас, то наши оценки расстояний окажутся заниженными. Кроме того, в одном из сценариев, предложенном Дж. П. Острайкером и С.Д. Тримейном из Принстона, предполагается, что галактики могут эволюционировать не только за счет эволюции имеющихся в них звезд, но и благодаря поглощению мелких соседних галактик! Уверен, пройдет еще немало времени, прежде чем мы получим количественные инструменты, позволяющие описать различные виды галактической эволюции.




