Для рассматриваемого в этой книге сценария важно, что Вселенная однажды пребывала в термодинамическом равновесии. Согласно статистической физике, свойства системы, находящейся в равновесии, полностью определяются температурой и несколькими сохраняющимися величинами (подробнее – в следующей главе). То есть мироздание хранит лишь выборочную информацию о начальных условиях. Если мы хотим узнать, что происходило в самом начале, этот факт играет против нас. Но, с другой стороны, мы избавлены от необходимости изобретать многочисленные гипотезы для установления хода космической истории.
Как уже говорилось выше, считается, что реликтовое излучение, открытое Пензиасом и Вильсоном, осталось во Вселенной с тех времен, когда она пребывала в равновесном состоянии. Следовательно, чтобы понять, какие свойства микроволнового фона мы ожидаем увидеть в наблюдениях, нужно задаться вопросом: как обычно ведет себя излучение, находящееся в термодинамическом равновесии с веществом?
Как ни странно, именно этот вопрос положил начало квантовой теории и представлению об излучении как о потоке фотонов. К 1890-м гг. стало понятно: свойства равновесного излучения зависят только от температуры. Точнее, количество энергии излучения в единичном объеме и в заданном диапазоне длин волн вычисляется по универсальной формуле, переменными в которой являются только длина волны и температура. По ней же рассчитывается излучение в ящике с непрозрачными стенками – т. е. радиоастроном с ее помощью может определить «эквивалентную температуру» радиошума, который он регистрирует. Эта же по сути формула позволяет посчитать, сколько излучения каждой длины волны испускает за секунду с единицы своей площади полностью поглощающая поверхность. Поэтому-то такое излучение называют еще излучением абсолютно черного тела. Резюмируя вышесказанное, для чернотельного излучения характерна определенная зависимость энергии от длины волны, представленная универсальной формулой, в которую входит еще только температура. В 1890-х гг. на поиски этой формулы бросились самые горячие головы теоретической физики.
В последние недели XIX в. правильную формулу для вычисления излучения черного тела посчастливилось найти Максу Карлу Эрнсту Людвигу Планку. В графической форме догадка Планка показана на рис. 7 для температуры зарегистрированного реликтового шума – 3 К. На словах же формулу Планка можно описать следующим образом. В ящике, заполненном чернотельным излучением, энергия в заданном диапазоне длин волн сначала резко растет с увеличением длины волны, достигает максимума, а затем резко спадает. Так называемое планковское распределение носит универсальный характер – оно не зависит от природы вещества, с которым взаимодействует излучение, а определяется лишь его температурой. Сегодня термин «чернотельное излучение» применяют к любому излучению, распределение энергии которого по длинам волн описывается формулой Планка – и не важно, действительно ли оно испущено абсолютно черным телом или нет. Итак, по крайней мере в первый миллион лет или около того, когда излучение и вещество находились в термодинамическом равновесии, Вселенную, должно быть, заполняло чернотельное излучение с температурой, равной температуре окружающей материи.
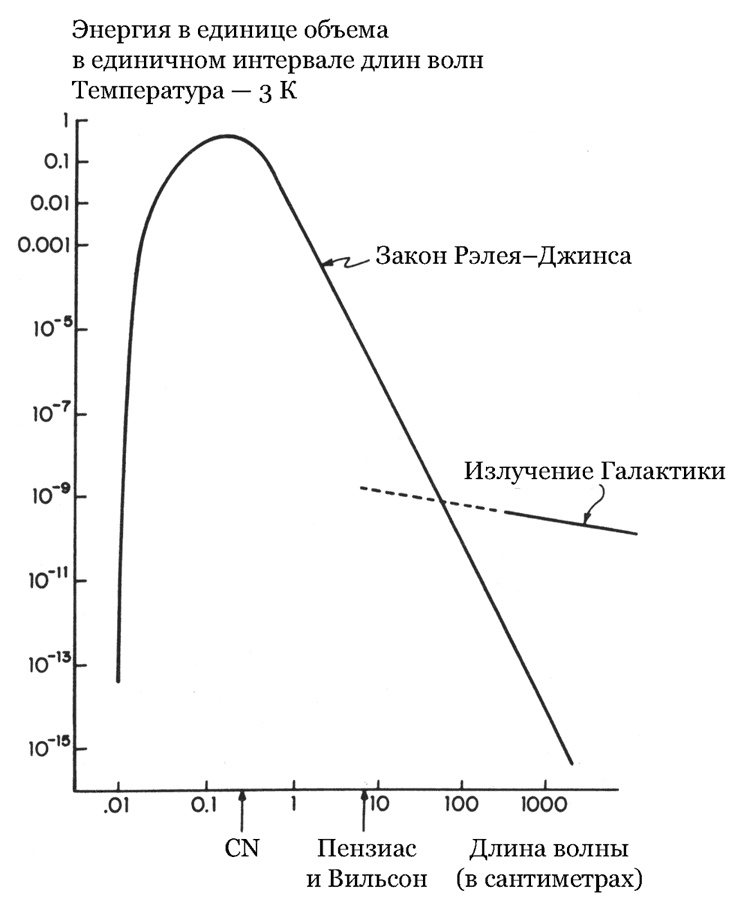
Рис. 7. Планковское распределение. На графике представлена зависимость плотности энергии чернотельного излучения в единичном интервале длин волн от длины волны для температуры 3 К. (Чтобы получить график для температуры, превышающей 3 К в f раз, достаточно сжать ось длин волн в 1/f раз, а вертикальную – растянуть в f 3 раз.) Прямой участок кривой с правой стороны описывается более простой формулой распределения Рэлея-Джинса. Помимо излучения черного тела, линия с таким наклоном возникает в самых разнообразных случаях. Крутой спад кривой слева объясняется квантовой природой излучения и является отличительной чертой излучения черного тела. Прямая с надписью «излучение Галактики» отображает интенсивность радиошума, испускаемого Млечным Путем. (Одна из стрелок указывает на длину волны, на которой Пензиас и Вильсон выполняли свои пионерские наблюдения, а второй отмечена длина волны, соответствующая возбуждению первого вращательного уровня молекулы межзвездного циана. Открыть реликтовый фон также можно было бы, заметив линию поглощения на этой длине волны.)
Значение открытия Планка простирается далеко за пределы проблемы излучения абсолютно черного тела: он первым предложил считать, что энергия поступает отдельными порциями, или квантами. Сам Планк предполагал, что разбивать на кусочки следует лишь энергию вещества, находящегося в равновесии с излучением. Однако несколькими годами позже Эйнштейн выдвинул гипотезу, что и само излучение существует в виде квантов (позже их стали называть фотонами). Этими-то идеями и вымощена дорога к одной из величайших в истории научной мысли революций, произошедшей в 1920-х гг.: на смену классической механике пришла квантовая.
В этой книге мы не собираемся излагать ее в деталях. Тем не менее, узнав, каким образом из идеи о фотонах следуют основные характеристики планковского распределения, можно лучше понять характер поведения излучения в расширяющейся Вселенной.
Спад графика плотности энергии в области больших длин волн объяснить легко: излучение с трудом помещается в ящике, размеры которого меньше длины волны. Об этом можно было догадаться (и догадались) и без квантовой теории – всего-навсего на основе старых представлений о волновой природе излучения.
А вот понять убывание плотности энергии чернотельного излучения при продвижении в сторону очень малых длин волн, оставаясь в рамках классической теории, нельзя. В статистической физике хорошо известно утверждение: при заданной температуре трудно произвести частицу, волну или еще какое-нибудь возбуждение, если ее энергия превосходит некоторое пороговое значение, прямо пропорциональное температуре. Получается, если волновые импульсы излучения могут иметь сколь угодно маленькую энергию, то на очень коротких волнах они беспрепятственно рождаются в сколь угодно больших количествах. Однако это не только противоречит экспериментальным данным, но и приводит к безумному утверждению о том, что полная энергия чернотельного излучения бесконечна! Единственным выходом было предположить, что энергия существует в виде отдельных порций (квантов) – причем чем меньше длина волны, тем больше энергии содержит одна порция. Тогда при любой заданной температуре в коротковолновой области будет наблюдаться дефицит излучения, поскольку отдельные порции в ней становятся очень энергонасыщенными. Окончательная формулировка этой гипотезы, предложенная Эйнштейном, звучит так: энергия фотона обратно пропорциональна длине волны. Следовательно, при заданной температуре в излучении черного тела очень мало фотонов с очень высокой энергией, а значит, почти нет фотонов со слишком маленькой длиной волны. Именно поэтому в планковском распределении виден спад в коротковолновой области.
Если переходить к цифрам, то энергия фотона с длиной волны 1 см равна 0,000124 электронвольта – и пропорционально увеличивается с уменьшением длины волны. Энергию фотонов удобно измерять в электронвольтах, каждый из которых равен энергии, набираемой электроном, прошедшим разность потенциалов в один вольт. Скажем, батарейка для фотовспышки на 1,5 вольта, проталкивая электроны по нити накала, затрачивает на каждый электрон 1,5 электронвольта энергии. (В системных единицах один электронвольт равен 1,602 × 10–12 эрг или 1,602 × 10–19 джоулей.) Как следует из правила Эйнштейна, энергия фотона микроволнового излучения с длиной волны 7,35 см, на которой работали Пензиас и Вильсон, равнялась 0,000124 электронвольта, деленного на 7,35 – т. е. 0,000017 электронвольта. А у типичного фотона видимого света длина волны составляет примерно двадцать тысячных сантиметра (5 × 10–5 см). Значит, его энергия равна 0,000124 электронвольта, умноженного на 20 000, – или 2,5 электронвольта. В любом случае с макроскопической точки зрения энергия фотона чрезвычайно мала, поэтому множество фотонов сливается для нас в непрерывный поток излучения.



