Имея в виду эти оговорки, космологи, однако, обычно предполагают, что лептонное число (количество электронов, мюонов и нейтрино за вычетом соответствующих античастиц) в расчете на фотон весьма невелико – во всяком случае, много меньше единицы. Такое заключение делается из соображений аналогии: если число барионов на фотон мало, то почему должно быть велико количество лептонов? Это одна из самых шатких гипотез стандартной модели. К счастью, даже если она неверна, на общую картину, которую мы здесь рисуем, она почти не повлияет.
Конечно, при температуре выше температурного порога для электронов лептонов и антилептонов было много – по своему количеству электроны и позитроны могли сравниться с фотонами. Кроме того, Вселенная была настолько горячей и плотной, что в таких условиях в тепловом равновесии находились даже юркие нейтрино – и их число тоже было сравнимо с количеством фотонов. Предпосылка, заложенная в стандартную модель, состоит в том, что разница в числе лептонов и антилептонов была и есть значительно меньше количества фотонов. Не исключено, что существовал небольшой избыток лептонов над антилептонами (как это имеет место в случае с барионами и антибарионами), который сохранился до сегодняшнего дня. Нейтрино и антинейтрино к тому же взаимодействуют так слабо, что многие из них, возможно, до сих пор не нашли себе партнера, чтобы аннигилировать. В этом случае в современной Вселенной их было бы примерно поровну и их количество было бы сравнимо с числом фотонов. В следующей главе мы увидим, что такой сценарий сегодня довольно популярен в космологии. Но не стоит и надеяться, что в обозримом будущем нам удастся зарегистрировать обширный океан нейтрино и антинейтрино.
Итак, вот наш рецепт ранней Вселенной. Возьмите заряд в расчете на фотон равным нулю, на каждый миллиард фотонов добавьте по одному бариону, а лептонное число примите равным некоторой малой величине. Задайте температуру в нужный вам момент времени как отношение современного размера Вселенной к размеру в интересующую вас эпоху, умноженное на 3 К (современная температура реликтового излучения). Хорошенько перемешайте, чтобы микроскопические распределения частиц различных сортов отвечали требованию теплового равновесия. Поместите все это во Вселенную, темп расширения которой определяется силой тяготения этого самого вещества. Если запастись терпением, то через некоторое время из этой мешанины должен получиться наш сегодняшний мир.
5. Первые три минуты
Итак, теперь мы достаточно подкованы, чтобы проследить за ходом космической эволюции в первые три минуты. Тогда события развивались гораздо стремительнее, чем сейчас, поэтому киноаппарат, показывающий кадры через равные промежутки времени, здесь не поможет. Вместо этого я синхронизую наш «фильм» с падающей температурой Вселенной, причем последовательные стоп-кадры по температуре будут различаться примерно в три раза.
К сожалению, у меня нет возможности начать показ с нулевого момента времени и бесконечной температуры. Известно, что, когда температура превысила порог в полторы тысячи миллиардов градусов (1,5 × 1012 К), во Вселенной в больших количествах появилась частица под названием пи-мезон. (Ее масса – около одной седьмой массы нуклона; см. таблицу I на с. 212.) В отличие от электронов, позитронов, мюонов и нейтрино, пи-мезоны очень сильно взаимодействуют с нуклонами и друг с другом. На самом деле как раз за счет обмена пи-мезонами нуклоны и держатся в атомном ядре. Когда появляется много таких сильновзаимодействующих частиц, описать поведение вещества при сверхвысоких температурах становится невероятно сложно. Поэтому, чтобы не вдаваться в хитроумные математические выкладки, в этой главе я начну повествование с первой сотой доли секунды. В этот момент температура составляла всего 100 миллиардов градусов Кельвина, что заведомо ниже пороговых значений для пи-мезонов, мюонов и остальных, более тяжелых частиц. В главе 7 кратко остановлюсь на том, что, по мнению физиков-теоретиков, могло происходить до этого момента.
Имея все это в виду, и начнем просмотр.
СТОП-КАДР № 1. Температура во Вселенной – 100 миллиардов градусов (1011 К). В этот момент космос проще для понимания, чем когда бы то ни было в будущем. Его заполняет однородный бульон из вещества и излучения, а каждая частица сталкивается с другими много-много раз в секунду. То есть, несмотря на стремительное расширение, Вселенная находится в почти идеально равновесном состоянии. Количество различных ингредиентов в ней, таким образом, определяется законами статистической физики и не зависит от того, что происходило до первого стопкадра. Нам достаточно знать, что температура равна 1011 К, а сохраняющиеся величины – заряд, барионное и лептонное число – очень маленькие или равны нулю.
В заметных количествах присутствуют только те частицы, чей температурный порог ниже 1011 К: электрон, позитрон и, конечно, безмассовые частицы, такие как фотон, нейтрино и антинейтрино (снова отсылаем читателя к таблице I на с. 212). Вещество во Вселенной упаковано настолько плотно, что даже нейтрино, которым ничего не стоит пройти сквозь свинцовую заслонку толщиной в несколько световых лет, находятся в тепловом равновесии с электронами, позитронами и фотонами и часто сталкиваются как с ними, так и друг с другом. (В понятие «нейтрино», напомню, я иногда включаю и антинейтрино.)
Упрощает картину и то, что температура 1011 К гораздо выше порога электронов и позитронов. Отсюда заключаем, что эти частицы – наряду с фотонами и нейтрино – ведут себя как излучение. Какова плотность энергии этих разновидностей излучения? Из таблицы I на с. 212 видим: вклад электронов и позитронов, вместе взятых, составляет 7/4 от энергии фотонов. Столько же вносят нейтрино с антинейтрино. Поэтому полная плотность энергии отличается от плотности энергии истинного излучения на коэффициент
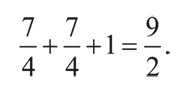
Из закона Стефана – Больцмана (см. главу 3) можно вычислить плотность энергии излучения при температуре 1011 К. Она оказывается равной 4,72 × 1044 электронвольт на литр. Значит, полная плотность энергии во Вселенной, нагретой до 1011 К, была в 9/2 раза больше – т. е. 21 × 1044 электронвольт на литр. Это эквивалентно массовой плотности в 3,8 миллиарда килограммов на литр, что в 3,8 миллиарда раз больше, чем плотность воды в земных условиях. (Когда я выражаю энергию в единицах массы, то, конечно, имею в виду ту энергию, которая выделилась бы согласно эйнштейновской формуле E = mc 2 – если бы вся масса перешла в энергию.) Если бы Эверест был сделан из такого плотного вещества, своим гравитационным полем он уничтожил бы Землю.
Вселенная, запечатленная на первом стоп-кадре, стремительно расширяется и охлаждается. При условии, что каждая ее частичка удаляется от произвольно выбранного центра со скоростью, равной скорости убегания, темп ее расширения легко посчитать. Из-за огромной плотности скорость убегания, естественно, тоже велика: характерное время расширения составляет примерно 0,02 с. (См. математическую заметку 3 на с. 237. В первом приближении характерное время расширения можно считать равным 100-кратному периоду, в течение которого размер Вселенной увеличивается на 1 %. Если говорить точнее, характерное время расширения – это величина, обратная постоянной Хаббла. Как отмечалось в главе 2, возраст Вселенной всегда меньше характерного времени расширения, поскольку из-за силы тяготения она расширяется все медленнее.)

