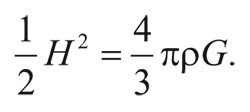Фазовый переход. Резкий переход системы из одной формы в другую – как правило, с изменением симметрии. В качестве примеров можно привести плавление, кипение и переход проводника в сверхпроводящее состояние.
Фейнмановские диаграммы. Диаграммы, обозначающие определенные математические выражения, возникающие при расчетах физических характеристик взаимодействия элементарных частиц.
Фотон. В квантовой теории излучения – частица, сопоставляемая со световой волной. Обозначается буквой γ.
Характерное время расширения. Величина, обратная постоянной Хаббла. Примерно равна стократному промежутку времени, за который размер Вселенной увеличивается на 1 %.
Цефеиды. Яркие переменные звезды, обладающие хорошо выраженной зависимостью между абсолютной светимостью, периодом изменения блеска и цветом. Свое название получили по имени звезды δ Цефея в созвездии Цефея (Царя). Служат инструментом измерения расстояний до относительно близких галактик.
Циан. Химическое соединение углерода и азота (CN). О наличии облаков циана в межзвездном пространстве можно судить по поглощению ими света.
Частота. Количество гребней волны, проходящих через данную точку в единицу времени. Равна скорости волны, деленной на ее длину. Измеряется в обратных секундах, или в герцах.
Электрон. Легчайшая из известных массивных частиц. Все химические свойства атомов и молекул определяются электрическим взаимодействием электронов с атомным ядром и друг с другом.
Электронвольт. Применяемая в атомной физике единица энергии, равная энергии, которую приобретает электрон, пройдя разность потенциалов в один вольт. Один электронвольт равен 1,60219 × 10–12 эрг.
Энергия покоя. Энергия покоящейся частицы, которая может высвободиться, если частица проаннигилирует. Вычисляется по формуле Эйнштейна: E = тс 2.
Энтропия. Фундаментальная физическая величина статистической физики, характеризующая степень беспорядка в физической системе. В процессах, не нарушающих термодинамическое равновесие, энтропия сохраняется. Второй закон термодинамики гласит, что в любых процессах полная энтропия остается постоянной либо возрастает.
Эрг. Единица энергии в системе СГС (сантиметр-граммсекунда), равная кинетической энергии тела массой один грамм, перемещающегося со скоростью один сантиметр в секунду. Один эрг равен одной десятимиллионной (10–7) джоуля.
Эффект Доплера. Изменение частоты сигнала, возникающее при относительном движении источника и приемника.
Ядерное равноправие. Парадигма, согласно которой все адроны одинаково фундаментальны.
Математическое приложение
Эти заметки предназначены для читателя, желающего вникнуть в математические выкладки, на которых зиждется описательное изложение материала данной книги. Их можно пропустить без ущерба для понимания сути.
Заметка 1. Эффект Доплера
Пусть гребни волны испускаются источником света через равные промежутки времени T. Если он удаляется от наблюдателя со скоростью V, то за время T, разделяющее два последовательных гребня, источник пройдет расстояние VT. Чтобы достичь наблюдателя, волна должна затратить дополнительное время VT/c, где с – скорость света. Таким образом, промежуток времени, через который наблюдатель регистрирует соседние гребни, равен
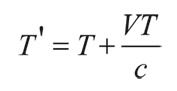
Длина волны испущенного света:
Длина волны принимаемого света:
Отношение этих длин:
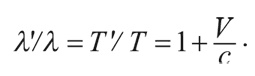
Предложенный вывод применим к случаю, когда источник движется по направлению к наблюдателю, за исключением того, что V меняется на – V. (Все вышесказанное справедливо в отношении любого волнового сигнала – не обязательно света.)
Например, скопления галактик в Деве удаляются от нас со скоростью 1000 км/с. Скорость света – 300 тысяч км/с. Следовательно, длина волны λ' любой из линий в спектре скопления больше ее номинального значения на коэффициент

Заметка 2. Критическая плотность
Рассмотрим сферу радиуса R, заполненную галактиками. (Для наших целей R должно быть больше расстояния между скоплениями галактик, но меньше длины, сравнимой с размером Вселенной в целом.) Масса, заключенная в этой сфере, равна ее объему, умноженному на плотность вещества ρ:
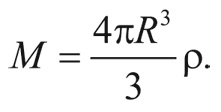
Согласно Ньютоновой теории всемирного тяготения, потенциальная энергия типичной галактики на поверхности этой сферы есть:
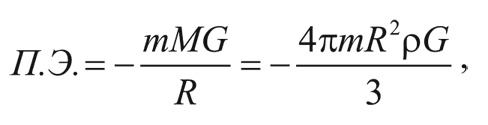
где m – масса галактики, а G – гравитационная постоянная Ньютона:
G = 6,67×10–8 см 3/(gm с 2).
Скорость этой галактики можно найти из закона Хаббла:
где H – постоянная Хаббла. Таким образом, кинетическая энергия равна:
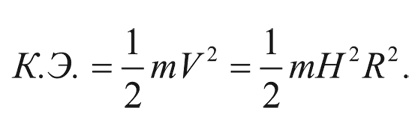
Полная энергия галактики – это сумма кинетической и потенциальной энергии:
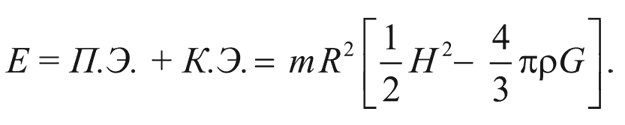
При расширении Вселенной эта величина должна оставаться неизменной.
Если E отрицательна, то галактика никогда не уйдет на бесконечность, поскольку на больших расстояниях потенциальной энергией можно пренебречь. Тогда полная энергия оказывается практически равной кинетической, а та, в свою очередь, всегда положительна. С другой стороны, если E положительна, то галактика может достичь бесконечности с некоторым запасом кинетической энергии. Таким образом, энергия E галактики, движущейся со скоростью убегания, по определению равна нулю. Откуда следует, что: