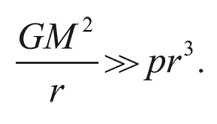Мы показали, что промежуток времени, за которой плотность падает от экстремальных значений, имевших место в ранней Вселенной, до ρ пропорционален, а сама плотность ρ пропорциональна 1/Rn. Время, следовательно, пропорционально Rn/2, или, что то же самое:

Эта формула остается в силе до тех пор, пока кинетическая и потенциальная энергии не упадут настолько, что достигнут одного порядка с их суммой – полной энергией.
Как было отмечено в главе 2, в любой момент времени t на расстоянии ct существует горизонт, отсекающий сигналы, которые еще не успели до нас дойти. Теперь мы увидели, что R(t) при t → 0 уменьшается медленнее, чем расстояние до горизонта. То есть в прошлом был момент, когда все «типичные» частицы находились за горизонтом.
Заметка 4. Излучение абсолютно черного тела
Согласно планковскому распределению энергия du чернотельного излучения в единице объема и в узком интервале длин волн от λ до λ + dλ равна:
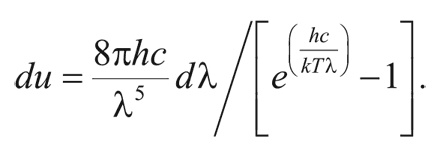
Здесь T – температура, k – постоянная Больцмана (1,38 × 10¯16 эрг/K), c – скорость света (299 729 км/с), e – число, равное 2,718…, и h – постоянная Планка (6,625 × 10¯27 эрг с), которую в эту формулу ввел Макс Планк.
В случае длинных волн для знаменателя в формуле Планка верно приближенное равенство:
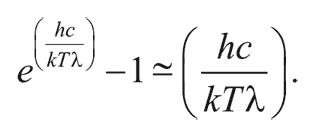
Таким образом, в данном диапазоне длин волн планковское распределение сводится к виду:
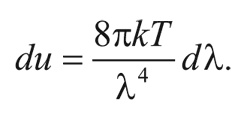
Эта формула выражает закон Рэлея – Джинса. Если бы он соблюдался для сколь угодно коротких волн, производная du/dλ стремилась бы к бесконечности при λ→0 и полная плотность энергии чернотельного излучения была бы бесконечной.
К счастью, планковское распределение достигает максимума при длине волны:
а затем на коротких волнах следует крутой спад. Полная плотность энергии излучения абсолютно черного тела выражается через интеграл:
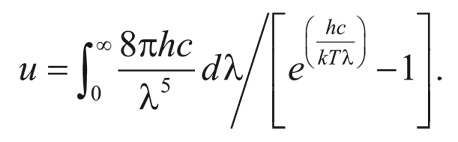
Интегралы такого вида легко найти в стандартных таблицах определенных интегралов. После интегрирования получаем:
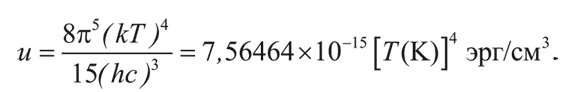
Эта формула выражает закон Стефана – Больцмана.
Распределение Планка легко переписать в терминах квантов света – фотонов. Энергия фотона вычисляется по формуле
Следовательно, число фотонов чернотельного излучения dN в единице объема и в узком интервале длин волн от λ до λ + dλ равно:
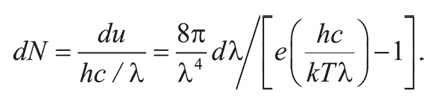
Тогда полное число фотонов в единице объема:
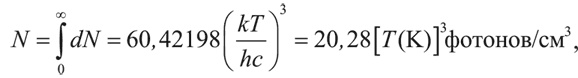
а средняя энергия фотона:
Еср. = и / N = 3,73 ×10¯16 [T (K)] эрг.
Теперь рассмотрим, что происходит с чернотельным излучением в расширяющейся Вселенной. Допустим, размер последней увеличился в f раз. Например, если Вселенная расширилась в два раза, то f = 2. Как мы знаем из главы 2, все длины волн пропорционально возрастут до значения:
В конечном состоянии плотность энергии du' в новом интервале длин волн от λ' до λ' + dλ' меньше по сравнению с первоначальной плотностью энергии du в старом диапазоне длин волн от λ до λ + dλ по двум причинам:
1. Поскольку объем Вселенной вырос в f 3 раз, а фотоны никуда не исчезают и ниоткуда не появляются, то их число в единице объема упало в 1/f 3 раз.
2. Энергия одного фотона обратно пропорциональна длине волны, и, значит, она уменьшилась в 1/f раз. Следовательно, полная плотность энергии уменьшилась в 1/f 4 раз (1/f 3 умножить на 1/f):
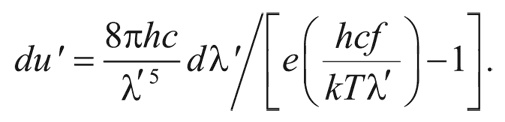
Переписывая эту формулу через новую длину волны λ', получим:
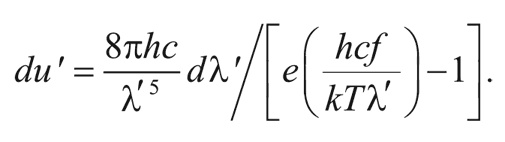
Но это опять та же самая формула для du в зависимости от λ и dλ, только вместо температуры Τ стоит новая температура:
Таким образом, приходим к заключению: свободно расширяющееся чернотельное излучение в любой момент времени описывается формулой Планка с температурой, обратно пропорциональной коэффициенту расширения.
Заметка 5. Масса Джинса
Чтобы из сгустка вещества образовалась гравитационно связанная система, его гравитационная потенциальная энергия должна превосходить энергию теплового движения. Гравитационная потенциальная энергия сгустка радиуса r и массы M по порядку величины равна:
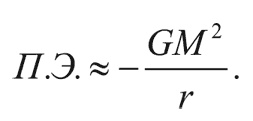
Внутренняя энергия в единице объема пропорциональна давлению р, поэтому полную внутреннюю энергию можно оценить как:
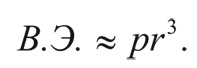
Гравитационные силы будут преобладать над силами давления, если