Но для заданной плотности ρ мы можем выразить r через M, пользуясь соотношением
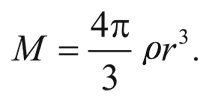
Таким образом, условие гравитационного скучивания приобретает вид
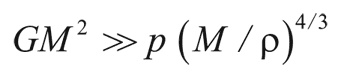
или по-другому:
где MJ (с точностью до несущественного численного множителя) называется массой Джинса:
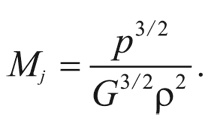
Например, непосредственно перед рекомбинацией водорода плотность равнялась 9,9 × 10¯22 г/см 3 (см. математическую заметку 3 на с. 237), а давление:
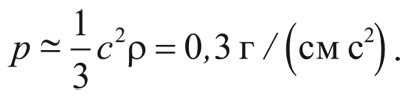
Следовательно, масса Джинса была:

Интересно отметить, что крупные шаровые скопления в нашей Галактике имеют примерно такую же массу.
Заметка 6. Температура и плотность нейтрино
Если тепловое равновесие не нарушается, в системе сохраняется физическая величина, известная как энтропия. Для наших целей достаточно будет воспользоваться приближенной формулой для энтропии S в единице объема при температуре T:
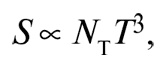
где ΝΤ – эффективное число сортов частиц, находящихся в тепловом равновесии, температурный порог которых ниже Τ. Чтобы сохранить энтропию на постоянном уровне, надо, чтобы S была обратно пропорциональна кубу размера Вселенной. Другими словами, если R – расстояние между любой парой типичных галактик, то:
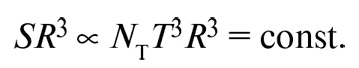
Незадолго до аннигиляции электронов и позитронов (при температуре около 5 × 109 K) нейтрино и антинейтрино уже вышли из теплового контакта с веществом во Вселенной, поэтому единственными частицами в тепловой бане оставались электрон, позитрон и фотон. Возьмем из таблицы I на с. 212 полное эффективное число сортов частиц до аннигиляции:
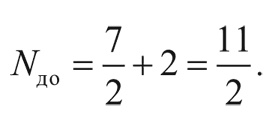
После того как в четвертом стоп-кадре электроны и позитроны аннигилировали, во Вселенной стали преобладать фотоны. Таким образом, число сортов стало:
Из сохранения энтропии следует, что:
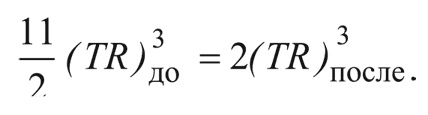
То есть тепло, выделившееся в процессе аннигиляции электронов и позитронов, приводит к повышению величины TR на коэффициент:
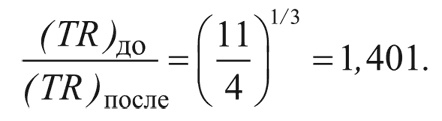
До аннигиляции электронов с позитронами температура нейтрино Τ была равна температуре фотонов Τ. Но затем Τv начала падать просто как 1/R, поэтому в любой последующий момент времени TvR равно значению TR до аннигиляции:
(TvR)после = (TvR)до = (TvR)до.
Отсюда заключаем: после завершения процесса аннигиляции температура фотонов превышает температуру нейтрино на коэффициент:
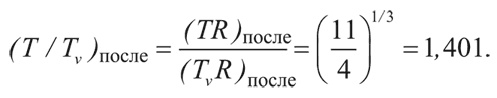
Хотя нейтрино и антинейтрино вышли из теплового равновесия, они вносят существенный вклад в полную плотность энергии. Эффективное число сортов нейтрино равно 7/2, т. е. 7/4 от числа степеней свободы фотона. (Фотон может находиться в двух состояниях с разным спином.) А температура нейтрино в четвертой степени, наоборот, в (4/11) 4/3 раза меньше температуры фотонов в четвертой степени. Соответственно отношение плотности энергии нейтрино и антинейтрино к плотности энергии фотонов равно:
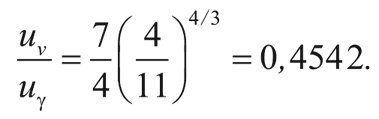
Из закона Стефана – Больцмана (см. главу 3) следует, что при температуре фотонов T плотность энергии фотонов есть:
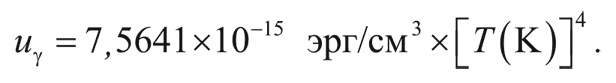
Таким образом, полная плотность энергии после аннигиляции электронов и позитронов равна:
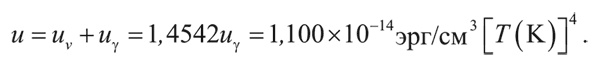
Эту величину можно пересчитать в массовую плотность, разделив первую на квадрат скорости света:
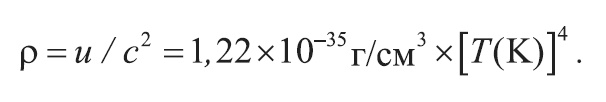
Послесловие. Что произошло в космологии с 1977 г.
За 16 лет, прошедших с момента первого издания «Первых трех минут», Вселенная расширилась на 12 стомиллионных процента. А может быть, только на 6,5 стомиллионных. Такой разброс данных связан с тем, что мы по-прежнему не очень точно знаем темп расширения Вселенной. Как говорилось в главе 2, он выражается через один из важнейших космологических параметров – постоянную Хаббла, которую измеряют, наблюдая зависимость скоростей далеких галактик от расстояния до них. В последнее время ошибки измерений, по словам астрономов, непрерывно уменьшаются. Однако разница между результатами различных групп, к сожалению, выходит за рамки заявленных погрешностей. По данным одних наблюдений, получена величина 80 км/с на мегапарсек (3,26 миллиона световых лет), а по другим, скорости галактик увеличиваются на 40 км/с на каждый мегапарсек. Получается, мы знаем темп расширения Вселенной всего лишь с точностью до двойки.
Проблема здесь не в измерении скоростей далеких галактик – это легко сделать, изучив смещение линий в спектре галактики в красную область. Трудности, как всегда, начинаются тогда, когда дело доходит до измерения дистанций. Раньше расстояния до галактик определяли, наблюдая некоторый класс объектов, характеризующихся постоянной собственной светимостью. Это, например, ярчайшие звезды или шаровые скопления в галактиках определенного класса, или, скажем, сверхновые. Зная их видимую светимость, можно вычислить расстояния до них. Чем они тусклее, тем дальше. Недавно на помощь пришли и другие методы, основанные на связи светимости какой-либо галактики с ее наблюдаемыми внутренними свойствами (такими, как скорости звезд и газовых облаков в галактике). Расстояния до галактик продолжают оценивать и по сверхновым, измеряя их видимую яркость. Как бы то ни было, полученные из разных наблюдений значения постоянной Хаббла противоречат друг другу. В свое время большие надежды возлагались на крупный «Космический телескоп Хаббла» (HST), расположенный на искусственном спутнике Земли. К сожалению, досадные технические проблемы, приводящие к недопустимым вибрациям зеркала и, как следствие, к искажению изображения, не позволили выполнять точные измерения расстояний до галактик. Хотя другим областям астрономии «Хаббл», несомненно, принес немало пользы.

