Если применить последний к каждой галактике, приходим к выводу: любой наблюдатель будет видеть одно и то же распределение скоростей остальных галактик независимо от того, в какой из них находится он сам. А элементарные математические выкладки показывают, что если этот принцип верен, то относительная скорость каждой пары галактик пропорциональна расстоянию между ними, что и наблюдал Хаббл.
Чтобы удостовериться в этом, рассмотрим три типичные галактики A, B и C, расположенные в ряд (рис. 1). Предположим, что расстояние между A и B такое же, как между B и C. Какова бы ни была скорость B, наблюдаемая в A, космологический принцип требует, чтобы у C была та же самая скорость относительно B. Но тогда, заметьте, галактика C, которая от A вдвое дальше, чем B, будет удаляться от A тоже в два раза быстрее, чем B. Таким же образом к этой цепочке можно добавлять все новые и новые галактики, и результат будет тем же: скорость разбегания любой пары галактик окажется пропорциональна расстоянию между ними.
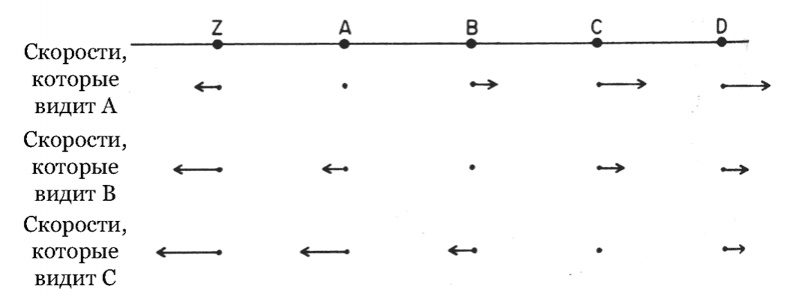
Рис. 1. Однородность и закон Хаббла. Здесь изображена цепочка равноудаленных друг от друга галактик A, B, C… Скорости, которые измеряют наблюдатели в A, B и C, показаны стрелками, имеющими определенные направление и длину. Принцип однородности требует, чтобы скорость галактики C, которую наблюдает B, равнялась скорости галактики B, которую наблюдает A. Складывая эти два значения, получаем скорость C, которую наблюдает A, – она представлена стрелкой вдвое большей длины. Продолжая в том же духе, можно изобразить полное распределение скоростей, представленное на рисунке. Как видно, их величины подчиняются закону Хаббла: скорость одной галактики, измеряемая наблюдателем в любой другой, пропорциональна расстоянию между ними. Это – единственное распределение скоростей, которое не противоречит принципу однородности
Как это часто бывает в науке, сей факт можно использовать и как следствие, и как предпосылку. Наблюдения Хаббла косвенно подтвердили справедливость космологического принципа. С философской точки зрения это весьма привлекательный вариант: нет причин полагать, что разные области Вселенной или разные направления в ней отличаются друг от друга. Кроме того, закон Хаббла подкрепляет нашу уверенность в том, что речь идет не о местном порыве ветра в космическом циклоне, а о довольно обширной области Вселенной. И наоборот, мы можем принять истинность космологического принципа a priori и вывести из него прямую пропорциональность между расстоянием и скоростью, как это было сделано выше. В любом случае, производя сравнительно несложную процедуру измерения доплеровских смещений, мы можем по скоростям давать оценки расстояний до очень далеких объектов. В пользу космологического принципа говорят и другие, не связанные с эффектом Доплера наблюдательные доводы. Если не обращать внимания на очевидные искажения, вносимые Млечным Путем и близким к нам большим скоплением галактик в созвездии Девы, Вселенная с Земли выглядит невероятно изотропной. Другими словами, она одинакова по всем направлениям. (Об этом недвусмысленно говорит и реликтовое излучение, речь о котором пойдет в следующей главе.) Еще Коперник учил: довольно неосмотрительно предполагать, будто человечество занимает во Вселенной какое-то обособленное место. Поэтому, если Вселенная изотропна рядом с нами, она, скорее всего, изотропна и для наблюдателей во всех типичных галактиках. Кроме того, последовательными вращениями вокруг разных центров каждую точку Вселенной можно перевести в любую другую точку (рис. 2). Соответственно, если Вселенная изотропна вокруг любой точки, она с необходимостью однородна.
Прежде чем двинуться дальше, сделаем ряд оговорок по поводу космологического принципа. Во-первых, он, очевидно, несправедлив на малых расстояниях. Мы сами находимся в галактике, входящей в небольшую местную группу галактик (среди них – M31 и M33), а та, в свою очередь, принадлежит к гигантскому скоплению галактик в созвездии Девы. К слову, из 33 галактик каталога Мессье почти половина располагаются в одном маленьком участке неба в Деве. Космологический же принцип, если он вообще верен, приобретает смысл, только если использовать масштабы, сравнимые с расстоянием между скоплениями галактик (около 100 миллионов световых лет).
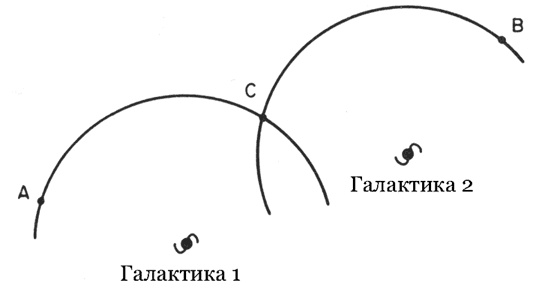
Рис. 2. Изотропия и однородность. Если Вселенная изотропна как вокруг галактики 1, так и вокруг галактики 2, то она однородна. Чтобы показать одинаковость свойств точек A и B, нарисуем две окружности: первая – с центром в галактике 1 – проходит через точку A, а вторая – с центром в галактике 2 – через точку B. Поскольку пространство вокруг галактики 1 изотропно, свойства точек A и C (точка пересечения двух окружностей) одинаковы. Аналогично из эквивалентности различных направлений вокруг галактики 2 следует эквивалентность свойств точек B и C. Следовательно, точки A и B также обладают одинаковыми свойствами
Вторая оговорка касается сложения скоростей. При применении космологического принципа для выведения прямой пропорциональности между скоростями галактик и расстояниями между ними мы предположили, что если скорость C относительно B совпадает со скоростью B относительно A, то скорость C относительно A будет в два раза больше. Это знакомое всем обычное правило сложения скоростей, которое безусловно работает для их малых значений, встречающихся в повседневной жизни. Оно, однако, обязано нарушаться для величин, сравнимых со скоростью света (300 тысяч км/с). В противном случае, складывая произвольное количество относительных скоростей, мы бы получили показатель, превышающий скорость света, что в специальной теории относительности Эйнштейна запрещено. Например, пусть пассажир самолета, летящего со скоростью в 3/4 скорости света, выстреливает по ходу движения пулей, набравшей тоже три четверти скорости света. Какова скорость пули относительно Земли? Обычное правило дает ответ: «полторы скорости света». Но это невозможно. В специальной теории относительности подобный нелепый ответ исключается путем изменения самого правила сложения скоростей. На самом деле скорость C относительно A несколько меньше, чем сумма скоростей B относительно A и C относительно B. Поэтому, сколько ни складывай скорости, меньшие скорости света, больше последней никак не получится.
Впрочем, в 1929 г. Хаббла эти проблемы не волновали. Все наблюдаемые им галактики имели скорости, ничтожные по сравнению со скоростью света. Однако, когда космологи работают с огромными расстояниями, которые во Вселенной встречаются сплошь и рядом, им не обойтись без теоретических схем, где указано, как обращаться со скоростями, близкими к световой. Такие рецепты дают общая и специальная теории относительности Эйнштейна. На подобных невообразимых расстояниях неоднозначным становится само понятие расстояния. Поэтому всегда надо уточнять, какое именно расстояние подразумевается: измеренное по светимости, угловым диаметрам, собственным движениям или по чему-то еще.
Но вернемся в 1929 год. Хаббл оценивал расстояния до 18 галактик по видимой светимости их ярчайших звезд, а затем сопоставлял их с соответствующими скоростями, найденными из спектроскопических измерений эффекта Доплера. Таким образом он пришел к заключению, что между скоростями и расстояниями имеется линейная зависимость (т. е. они пропорциональны друг другу). Честно говоря, глядя на данные Хаббла, я несколько недоумеваю: как он вообще пришел к этому заключению? Скорости галактик разбросаны почти случайно – угадывается лишь слабый намек на их увеличение с расстоянием. Более того, для этих 18 галактик вряд ли можно ожидать четкой зависимости между скоростью и расстоянием: все они находятся слишком близко к Земле (во всяком случае, не дальше скопления в Деве). Сам собой напрашивается вывод, что Хаббл – руководствовался ли он простыми аргументами, изложенными выше, или положениями теорий, которые мы еще обсудим, – знал ответ заранее.




