8.4. Сверхновая Тихо Браге
Любой электронный планетарий поможет вам восстановить картину той ночи. Если в вашей программе не обозначена Nova Tycho, то ее приблизительные координаты 0h, +62°. В эти дни Тихо жил в Швеции, в местечке с координатами 56° с. ш., 13° в. д.
Как видим, ночное небо в тот период было очень привлекательным для астронома: Луна приближалась к первой четверти и еще не засвечивала небо, к полуночи высоко поднимался яркий (−3m) Юпитер. А новая звезда сияла недалеко от зенита. Не заметить ее было просто невозможно, поскольку располагалась она прямо внутри астеризма «W» Кассиопеи. В конце ночи поднималась Венера, а в лучах утренней зори восходил Меркурий.
Под утро, когда Венера была уже на высоте 20°, Nova опускалась на севере до 30°. Сравнивать их блеск было удобно. До полудня Nova проходила через нижнюю кульминацию на высоте около 28° и к вечеру вновь поднималась над горизонтом к высоте 70°. Трудно было бы ожидать более удобных условий для наблюдения этого замечательного события — взрыва сверхновой звезды в эпоху рождения современной науки. А самое приятное и неожиданное, что в те дни поздней осени над Северной Европой было ясное небо!
8.5. Сверхновая Кеплера
В эти дни было редкое сочетание планет: в южной части Змееносца на расстоянии всего нескольких градусов друг от друга сошлись Юпитер, Сатурн и Марс, притягивая к себе внимание астрономов. И в этом же месте вспыхнула сверхновая! Правда, вся эта компания ярких светил скрывалась на юго-западе под горизонтом вскоре после захода Солнца. Луна в эти дни была близка к полнолунию и уже довольно высоко поднималась на востоке. Оценить блеск сверхновой удавалось именно благодаря ее близости к ярким планетам. Во второй половине дня Сверхновая Кеплера кульминировала на высоте около 18° над горизонтом, что делало ее дневное наблюдение весьма непростым делом.
После этих двух вспышек сверхновых — Тихо и Кеплера — прошло три века, пока в 1885 г. на земном небосклоне люди вновь заметили вспышку сверхновой, но уже в соседней галактике Туманность Андромеды (S Andomedae, 6m). Скорее всего, она осталась бы незамеченной, если бы в те годы астрономы уже активно не пользовались телескопами. Следующую сверхновую невооруженным глазом увидели лишь четыре века спустя — в 1987 г. Она вспыхнула совсем недалеко от нашей Галактики, в Большом Магеллановом Облаке, и в максимуме блеска достигла +2,9m.
8.6. Хаббл на шаре
Расстояние между точками на сфере D = αR, где α — центральный угол, R — радиус сферы. Скорость взаимного удаления точек
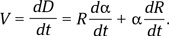
Но для любой пары точек dα/dt = 0. Поэтому
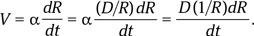
Но (1/R)dR/dt для всех точек на шаре одинаково, поэтому в любой фиксированный момент времени V ~ D.
Для модели в виде точек на поверхности надуваемого шара закон Хаббла справедлив.
8.7. Отверстие в небе
Гюйгенс открыл Большую туманность Ориона, известную сегодня всем любителям астрономии. Позднее выяснилось, что до Гюйгенса, возможно первым в Европе, в 1618 г. эту туманность наблюдал в телескоп швейцарский астроном Иоганн Цизат (1586–1657), но не обратил на это должного внимания.
8.8. Путешествие света
Красным смещением называют относительное изменение длины волны линий в спектре удаляющейся галактики: z ≡ Δλ/λ. Оно возникает в результате эффекта Доплера. Если скорость удаления галактики значительно меньше скорости света (v ≪ c), то эффект Доплера описывается очень простой формулой: Δλ/λ = v/c. Отсюда v = cz.

Закон Хаббла говорит, что скорость удаления галактики и расстояние до нее (D) связаны линейной зависимостью: v = H0D. Следовательно, D = cz/H0. А время путешествия света от галактики до наблюдателя составит t = D/c = z/H0.
Осталось вычислить значение H-10. Как известно, 1 парсек = 206 265 а. е. = 206 265 · 150 млн км = 3,1 · 1013 км. А 1 Мпк = 106 пк. Дальше совсем просто:
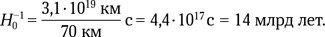
Итак, если красное смещение линий в спектре галактики равно z и при этом не очень велико (скажем, не более 0,2 · 0,3), то свет от нее до наблюдателя путешествовал t = z · 14 млрд лет.
8.9. «Гайя» смотрит на Солнце
Радиус орбиты Юпитера 5,2 а. е., а его масса в 1000 раз меньше солнечной, значит, полный размах колебаний Солнца относительно их общего с Юпитером центра масс составляет 10,4 а. е./1000. Отрезок в 1 а. е. с расстояния в 1 пк виден под углом в 1″ (по определению парсека). Значит, отрезок в (10,4/1000) а. е. под углом в 0,00002″ будет виден с расстояния (10,4/1000)/0,00002 = 520 пк.
8.10. Андромеда и Треугольник
Угловое расстояние на небе между галактиками М31 и М33 составляет 14,8°. Расстояние до М31 оценивается в 778±33 кпк. Расстояние до М33 оценивается со значительно меньшей точностью: от 730 до 940 кпк. Поэтому минимальным расстоянием между ними в пространстве будет такое, при котором мы будем считать их на одинаковом расстоянии от Земли. Пусть это будет расстояние до М31 (778 км), поскольку оно известно лучше. Учитывая невысокую точность измеренных расстояний, угол 14,8° можно считать небольшим по сравнению с радианом (≈ 57,3°) и ограничиться простой пропорцией: минимальное расстояние между галактиками составляет 778 кпк − (14,8/57,3) ≈ 200 кпк.
8.11. Сколько скоплений в Галактике
Диск Галактики — плоская звездная система с характерной толщиной существенно меньше чем 3 кпк. Поэтому наши наблюдения «вырезают» из него не сферу, а круг радиусом 3 кпк, составляющий от полной площади диска (3/18)2 = 1/36 часть. Если плотность числа звездных скоплений в других частях диска примерно такая же, как в окрестности Солнца, то всего в диске 1500 · 36 = 54 000 скоплений.

