Поиск маршрута на карте — очевидный и всем известный пример, но, возможно, недостаточно объективный, поскольку отдельных локаций очень мало. Например, в США имеется лишь около 10 млн перекрестков. Казалось бы, большое число, но это ничто по сравнению с количеством отдельных позиций в пятнашках. Пятнашки — это игра с сеткой 4 × 4, где находятся 15 пронумерованных фишек и пустое место. Перемещая фишки, нужно достичь целевой конфигурации, скажем, расположить их все по порядку номеров. В пятнашках около 10 трлн состояний (в миллион раз больше, чем перекрестков в США!); пазл с 24 клетками допускает около 8 триллионов триллионов состояний. Это пример того, что в математике называется комбинаторной сложностью, — очень быстрого увеличения количества комбинаций с ростом числа «подвижных элементов» задачи. Вернемся к карте США: если компания-грузоперевозчик хочет оптимизировать движение 100 своих грузовиков по территории страны, количество возможных состояний составит 10700.
Отказ от надежды на рациональные решения
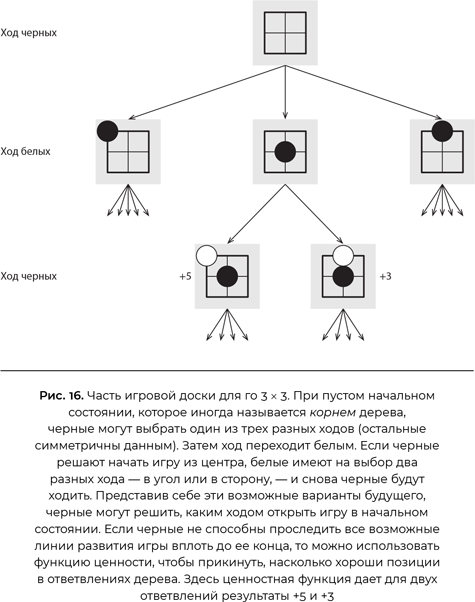
Многие игры отличаются комбинаторной сложностью, в том числе шахматы, шашки, нарды и го. Поскольку правила го просты и изящны (рис. 15), я использую эту игру для примера. Задача сформулирована четко: выиграть, окружив больше территории, чем противник. Возможные действия также понятны: клади камень на свободное пересечение. Как и в случае навигации по карте, очевидный способ принятия решения о действии состоит в том, чтобы представить разные варианты будущего, вытекающие из разных последовательностей действий, и выбрать наилучший. Вы спрашиваете себя: «Если я сделаю это, как может поступить мой противник? Что я сделаю тогда?» Эта мысль продемонстрирована на рис. 16 на примере го размерности 3 × 3. Даже для доски 3 × 3 я могу показать лишь малую часть возможных вариантов будущего, но, надеюсь, мысль ясна. Действительно, этот способ принятия решений кажется проявлением самого обычного здравого смысла.
Проблема в том, что в го существует более 10170 возможных позиций для полноразмерной доски 19 × 19. Если найти гарантированно кратчайший маршрут на карте относительно легко, найти гарантированную победу в го почти нереально. Даже если гонять алгоритм миллиард лет, он сможет исследовать лишь крохотную часть полного дерева возможностей. Отсюда вытекает два вопроса. Первый: какую часть дерева должна исследовать программа? Второй: какой ход она должна сделать, исходя из той части древа, которую исследовала?

Сначала ответим на второй вопрос. Основная идея, используемая практически во всех прогностических программах, состоит в том, чтобы приписывать оценку ценности ответвлениям дерева — самым отдаленным будущим состояниям — и затем двигаться назад, выясняя, насколько хороши варианты выбора ближе к корню
[336]. Например, посмотрев на две позиции в нижней части схемы на рис. 16, можно дать оценку +5 (с точки зрения черных) позиции слева и +3 позиции справа, поскольку камень белых в углу намного более уязвим, чем сбоку. Если эти оценки верны, то черные могут ожидать от белых хода вбок, что приведет к позиции, представленной справа; следовательно, разумно приписать ценность +3 начальному ходу черных в центр. С небольшими вариациями это схема, использованная шахматной программой Артура Самуэля, победившей своего создателя в 1955 г.
[337], Deep Blue, обыгравшей чемпиона мира по шахматам Гарри Каспарова в 1997 г., и AlphaGo, одолевшей бывшего чемпиона мира по го Ли Седоля в 2016 г. Для Deep Blue написали фрагмент программы, оценивавший позиции как ответвлений, на основании, главным образом, своего собственного знания шахмат. Программы Самуэля и AlphaGo изучили их сами по опыту тысяч или миллионов тренировочных игр.
Первый вопрос — какую часть дерева должна исследовать программа — является примером одного из самых важных вопросов в сфере ИИ: какие вычисления должен делать агент? В случае игровых программ это жизненно важно, поскольку они располагают малым, фиксированным временем, и тратить его на бесцельные расчеты — верный путь к проигрышу. Для людей и других агентов, действующих в реальном мире, это еще важнее, потому что реальный мир несравненно сложнее: без качественного выбора никакое количество вычислений не сделает ни малейшей зарубки в проблеме принятия решения о том, как действовать. Если вы ведете машину и на дорогу выходит лось, нет смысла размышлять о том, следует ли обменять евро на фунты стерлингов или черным сделать первый ход в середину доски.
Способность людей управлять своей вычислительной деятельностью так, чтобы принимать разумные решения в разумное время, по меньшей мере столь же потрясающа, как и их способность верно воспринимать информацию и рассуждать. Представляется, что мы приобретаем ее естественно и без усилий. Когда отец учил меня играть в шахматы, то объяснил мне правила, но не учил конкретным умным алгоритмам выбора, какую часть дерева исследовать, а какую игнорировать.
Как это происходит? На основании чего мы направляем ход своих мыслей? Ответ заключается в том, что вычисление ценно лишь постольку, поскольку повышает качество ваших решений. Процесс выбора вычислений называется метарассуждением, что означает рассуждение о рассуждении. Как действия можно выбирать рационально, исходя из ожидаемой ценности, так и вычисления. Это так называемое рациональное метарассуждение
[338]. Оно строится на очень простой идее:





