
Приложение Г. Обучение на опыте
Обучение — это повышение результативности на основе опыта. Для системы зрительного восприятия это может означать обучение распознаванию большего числа категорий объектов с опорой на наблюдаемые примеры этих категорий. Для систем, основанных на опыте, само приобретение дополнительного знания является обучением, потому что означает, что система сумеет ответить на большее количество вопросов. Для прогностической системы принятия решений, такой как AlphaGo, обучение может означать повышение ее способности оценивать игровую позицию или исследовать полезные части дерева возможностей.
Обучение на примерах
Самая распространенная форма машинного обучения называется контролируемым обучением, или обучением с учителем. Алгоритм контролируемого обучения получает набор упражнений, для каждого из которых указан правильный ответ, и должен сформировать гипотезу о том, в чем состоит правило. Обычно система контролируемого обучения стремится оптимизировать соглашение между гипотезой и учебными образцами. Часто также вводится штраф за более сложную, чем это необходимо, гипотезу, в соответствии с принципом Оккама.
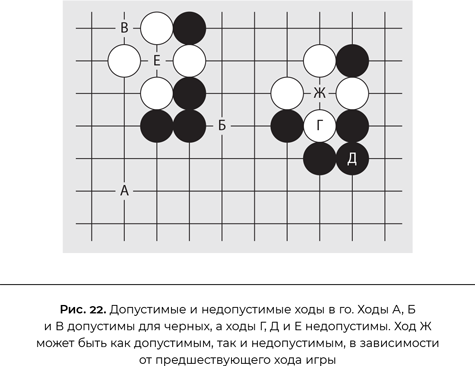
Проиллюстрируем это на задаче изучения допустимых ходов в го. (Если вы знаете правила го, вам будет проще следить за ходом рассуждений, если нет — легче проникнуться сочувствием к обучающейся программе.) Допустим, алгоритм начинает с гипотезы:
для всех временных шагов t и для всех местоположений l
допустимо выставить камень на местоположение l в момент времени t.
В позиции, представленной на рис. 22, ход черных. Алгоритм пробует ход А — все хорошо. Б и В тоже. Затем программа пробует совершить ход Г, поставив камень поверх уже лежащего белого камня: он недопустим. (В шахматах или нардах так можно было бы ходить, именно так «съедаются» фигуры.) Ход Д, поверх черного камня, также недопустим. (Недопустим и в шахматах, но допустим в нардах.) На этих пяти учебных примерах алгоритм может построить следующую гипотезу:
для всех временных шагов t и для всех местоположений l
если l не занято в момент времени t,
то допустимо выставить камень на местоположение l в момент времени t.
Затем программа пробует ход Е и, к своему удивлению, обнаруживает, что он недопустим. После несколько фальстартов она приходит к выводу:
для всех временных шагов t и для всех местоположений l
если l не занято в момент времени t
и l не окружено камнями противника,
то допустимо выставить камень на местоположение l в момент времени t.
(Иногда в го это правило называется запретом самоубийства.) Наконец, она проверяет ход Ж, который в этом случае оказывается допустимым. Почесав затылок и, возможно, еще немного поэкспериментировав, программа останавливается на гипотезе, что Ж годится, несмотря на то что камень окружен, потому что захватывает белый камень на Г и сразу же становится не окруженным.
Как видно из постепенного развития правил, обучение происходит через последовательность модификаций гипотезы, так чтобы она соответствовала наблюдаемым примерам. Обучающийся алгоритм делает это с легкостью. Исследователи машинного обучения разработали всевозможные остроумные алгоритмы быстрого поиска хороших гипотез. В данном случае алгоритм ведет поиск в пространстве логических выражений, представляющих правила го, но гипотезы могут являться и алгебраическими выражениями, представляющими физические законы, вероятностными Байесовыми сетями, представляющими заболевания и симптомы, или даже компьютерными программами, определяющими сложное поведение какой-то другой машины.
Второй важный момент состоит в том, что даже хорошая гипотеза может быть неверной. На самом деле, вышеприведенная гипотеза неверна, даже после внесения исправления о том, что ход Ж является допустимым. Она должна включать правило ко, или отсутствия повторов. Например, если белые только что захватили черный камень на Ж, сделав ход на Г, то черные не могут сделать перезахват, пойдя на Ж, поскольку создается та же позиция. Обратите внимание, что это правило резко отличается от того, что программа выучила к настоящему моменту, поскольку означает, что допустимость не может определяться текущей позицией, необходимо помнить и предыдущие.
Шотландский философ Дэвид Юм заметил в 1748 г., что индуктивное рассуждение — а именно от конкретного наблюдения к общим принципам, — не может гарантировать истинности вывода
[360]. Современная теория статистического обучения не требует гарантий абсолютной истинности, а лишь гарантию того, что найденная гипотеза, вероятно, является приблизительно правильной
[361]. Обучающемуся алгоритму может «не повезти» наткнуться на нерепрезентативную выборку, например он так и не попробует сделать ход на Ж, считая его недопустимым. Возможно также, что он не сумеет предсказать какие-нибудь редкие пограничные случаи, скажем, охватываемые какими-то более сложными и редко всплывающими разновидностями правила отсутствия повторов
[362]. Однако, поскольку Вселенная проявляет определенную степень регулярности, крайне маловероятно, чтобы алгоритм выработал чрезвычайно плохую гипотезу, потому что такая гипотеза почти наверняка была бы отброшена одним из экспериментов.
Глубокое обучение — метод, вызывающий в СМИ всю эту шумиху по поводу ИИ, — является, главным образом, формой контролируемого обучения. Это одно из самых существенных достижений в сфере ИИ за последние десятилетия, поэтому полезно разобраться, как он работает. Более того, некоторые исследователи убеждены, что этот метод позволит создать ИИ-системы человеческого уровня в течение нескольких лет, так что стоит оценить, насколько это вероятно.




