вероятность случайного совпадения: при судебной экспертизе ДНК – вероятность того, что человек, случайно выбранный из надлежащей популяции, будет соответствовать найденной ДНК в степени, которая связывает подозреваемого и преступление;
внешняя валидность: когда заключения исследования можно обобщать на целевую совокупность, которая шире, чем непосредственно исследуемая совокупность. Относится к релевантности исследования;
внутренняя валидность: когда заключения какого-либо исследования действительно касаются только изучаемой совокупности. Это относится к строгости, с которой проведено исследование;
воздействие: фактор, влияние которого на заболевание, смерть или иной медицинский исход, представляет для нас интерес, например какой-то аспект окружающей среды или поведения;
возмущающий (искажающий) фактор: переменная, которая связана и с предикторной переменной, и с переменной отклика и может объяснить часть их видимой взаимосвязи. Например, рост и вес детей сильно коррелированы, но в основном эта взаимосвязь объясняется возрастом ребенка;
воронкообразный график: график, где наблюдениям, соответствующим отдельным элементам (учреждения, области или исследования), сопоставляется мера их точности. Часто две «воронки» указывают на то, где можно ожидать месторасположения 95 % и 99,8 % наблюдений, когда между элементами в действительности нет разницы. Если распределение наблюдений приближенно нормальное, то граничные значения для 95 % и 99,8 % примерно соответствуют ±2 и ±3 стандартным ошибкам;
выборочное среднее: см. среднее 2.
генеральная совокупность (популяция): группа, из которой, как предполагается, берутся данные в выборке и которая дает вероятностное распределение для отдельного наблюдения. При проведении измерений или наличии у вас всех возможных данных это понятие становится математической идеализацией;
глубокое обучение: метод машинного обучения, который расширяет стандартные модели искусственных нейронных сетей на множество слоев, представляющих различные уровни абстракции, например переход от отдельных пикселей изображения к распознанию объектов;
гипергеометрическое распределение: пусть имеется конечное множество из N элементов, K из которых обладают некоторым свойством. Мы выбираем n элементов без возвращения. Тогда случайная величина Y – число успехов (выбранных элементов с этим свойством) имеет гипергеометрическое распределение. Формально для k = 0,1,…,n
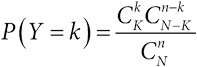
грамотность в работе с данными: умение понимать принципы, лежащие в основе работы с данными, выполнять базовые анализы данных, критически анализировать качества утверждений, сделанных на основе данных;
дерево классификации: форма алгоритма классификации, при котором характеристики проверяются последовательно; ответ на очередной вопрос определяет, какая характеристика проверяется следующей; процедура повторяется до итоговой классификации;
дилемма смещения – дисперсии: когда для прогноза используется обучение модели, повышение ее сложности в итоге приводит к тому, что у модели уменьшается смещение (в том смысле, что у нее возрастает потенциал для адаптации к деталям базового процесса), но увеличивается дисперсия, поскольку данных для уверенности в параметрах модели оказывается недостаточно. Чтобы избежать переобучения, нужен компромисс;
дисперсия выборочная: если имеется выборка x1,x2,…,xn со средним
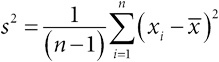 , то выборочная дисперсия (хотя знаменатель может быть равен n, а не n−1)
[279];
, то выборочная дисперсия (хотя знаменатель может быть равен n, а не n−1)
[279];
дисперсия: характеристика разброса случайной величины; если случайная величина X имеет математическое ожидание E(X) = μ, то дисперсия D(X) = E(X−μ)2 Среднеквадратичное (стандартное) отклонение является корнем из дисперсии, так что
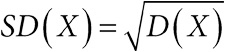 ;
;
доверительный интервал: оцениваемый интервал, в котором может находиться неизвестный параметр. Например, при наличии наблюдаемого множества данных x 95-процентный доверительный интервал для среднего μ – это такой интервал от L(x) до U(x), когда до наблюдения данных вероятность того, что случайный интервал (L(x),U(x)) содержит μ, составляет 95 %. Если соединить центральную предельную теорему с тем фактом, что примерно 95 % нормального распределения отклоняется от среднего не более чем на 2 стандартных отклонения, мы получим популярное приближение, что 95-процентный доверительный интервал – это оценка в ±2 стандартные ошибки. Предположим, что мы хотим найти доверительный интервал для разности μ2−μ1 между двумя параметрами μ2 и μ1. Если T1 – это оценка для μ1 со стандартной ошибкой SE2, а T2 – это оценка для μ2 со стандартной ошибкой SE2, то T2−T1 представляет собой оценку для μ2−μ1. Дисперсия разности между оценками равна сумме их дисперсий, и поэтому стандартная ошибка для T2−T1 определяется формулой
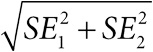 . Отсюда можно найти 95-процентный доверительный интервал для разности μ2−μ1;
. Отсюда можно найти 95-процентный доверительный интервал для разности μ2−μ1;
зависимая переменная (переменная отклика): переменная, которая представляет основной интерес, которую мы желаем спрогнозировать или объяснить;



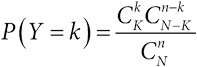
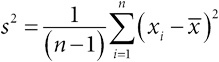 , то выборочная дисперсия (хотя знаменатель может быть равен n, а не n−1)
, то выборочная дисперсия (хотя знаменатель может быть равен n, а не n−1)
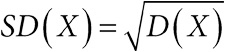 ;
;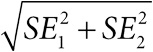 . Отсюда можно найти 95-процентный доверительный интервал для разности μ2−μ1;
. Отсюда можно найти 95-процентный доверительный интервал для разности μ2−μ1;