стандартная ошибка: стандартное отклонение выборочного среднего, когда оно рассматривается как случайная величина. Предположим, что X1, X2,…, Xn – это независимые одинаково распределенные случайные величины, взятые из распределения со средним μ и среднеквадратичным отклонением σ. Тогда их среднее Y = (X1 + X2 +…+ Xn)/n имеет среднее μ и дисперсию σ2/n. Стандартное отклонение для Y равно σ/√n и известно как стандартная ошибка. Оценкой будет s/√n, где s – выборочное стандартное отклонение для наблюдаемых величин X;
статистика: 1) дисциплина, занимающаяся изучением мира на основе данных; как правило, включает цикл решения проблем наподобие PPDAC; 2) какая-либо функция от данных. Например, наибольшее значение выборки, выборочное среднее, интерквартильный размах, выборочная дисперсия – различные статистики;
статистическая значимость: наблюдаемый эффект считается статистически значимым, когда P-значение, соответствующее нулевой гипотезе, меньше некоторого заранее установленного уровня, например 0,05 или 0,001. Это означает, что такой экстремальный результат маловероятен при справедливости нулевой гипотезы и всех прочих предположениях при моделировании;
статистическая модель: математическое представление вероятностного распределения какого-либо набора случайных величин, содержащее неизвестные параметры;
статистическое заключение: процесс использования данных выборки, для того чтобы что-либо узнать о неизвестных параметрах, лежащих в основе статистической модели;
стохастическая неопределенность: неизбежная непредсказуемость будущего, также известная как случайность, случай и так далее;
судебная эпидемиология: использование знаний о причинах заболеваний в популяциях при вынесении суждений о случаях болезни у отдельных людей;
счетные переменные: переменные, которые могут принимать целочисленные значения 0, 1, 2 и так далее или быть взаимнооднозначно сопоставлены с такими значениями;
тест перестановки/рандомизации: форма критерия для проверки гипотезы, когда распределение тестовой статистики при нулевой гипотезе получается не с помощью детальной статистической модели для случайных величин, а путем перестановки «меток» данных. Предположим, что нулевая гипотеза такова: какая-то «метка» (например, мужчина это или женщина) не связана с результатом обследования. Тесты рандомизации исследуют все возможные способы перестановки таких меток для отдельных элементов данных, при этом при нулевой гипотезе все они равновероятны. Для каждой перестановки вычисляется тестовая статистика, а P-значение определяется как доля тех перестановок, где получаются более экстремальные значения тестовой статистики, нежели реально наблюдаемые;
уровень ложноположительных результатов: при проверке многих гипотез доля положительных утверждений, которые оказываются ложноположительными;
фрейминг: выбор способа подачи информации, влияющего на впечатление аудитории;
центральная предельная теорема: общее название нескольких теорем, утверждающих, что при определенных условиях выборочное среднее для множества случайных величин сходится к нормальному распределению вне зависимости (за некоторыми исключениями) от исходного распределения этих случайных величин. Если у нас есть n независимых наблюдений с математическим ожиданием μ и дисперсией σ2, то при широких условиях их выборочное среднее является оценкой для μ и приближенно имеет нормальное распределение со средним μ, дисперсией σ2/n и среднеквадратичным отклонением σ√n (также известным как стандартная ошибка оценки);
цикл PPDAC: предлагаемая структура «цикла данных», куда входят проблема, планирование, сбор данных, анализ (поисковый или подтверждающий), заключение и коммуникация;
чувствительность: доля «положительных» случаев, которые правильно определены при классификации или тестировании; часто называется долей истинно положительных наблюдений. Единица минус чувствительность – это доля ложноотрицательных наблюдений (ошибка второго рода);
шансы, отношения шансов: если вероятность какого-то события равна p, то шансы для такого события определяются как
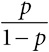. Если шансы для какого-то события в группе с воздействием равны
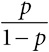, а шансы в группе без воздействия –
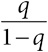, то отношение шансов составит
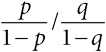. Если p и q малы, то отношение шансов близко к относительному риску p/q, но если абсолютные риски значительно превышают 20 %, то отношения шансов и относительные риски начинают различаться;
эпидемиология: изучение скорости распространения и причин заболеваемости;
эпистемическая неопределенность: недостаток знаний о фактах, числах или научных гипотезах.
Благодарности
Все идеи, возникающие в ходе долгой карьеры в статистике, – результат вдохновляющих бесед с коллегами. Хотя перечислить всех, у кого я их позаимствовал, сложно даже мне как статистику, короткий список я все же приведу, это Ники Бест, Шейла Бёрд, Дэвид Кокс, Филип Дэвид, Стивен Эванс, Эндрю Гельман, Тим Харфорд, Кевин Макконвей, Уэйн Олдфорд, Сильвия Ричардсон, Этан Шах, Адриан Смит и Крис Вайлд. Я искренне благодарен вам и многим другим людям за поддержку и вдохновение.
Из-за моей хронической прокрастинации процесс написания книги сильно затянулся. Поэтому я хотел бы поблагодарить Лору Стикни из издательства Penguin не только за заказ книги, но и за проявленное в течение всего этого времени спокойствие, сохраняемое даже тогда, когда работа была закончена, но мы все никак не могли договориться о названии. Спасибо Джонатану Пеггу за создание хороших условий, Джейн Бёрдселл за колоссальное терпение при редактировании и всему персоналу Penguin за кропотливую работу.
Я крайне признателен за разрешение использовать иллюстрации следующим людям и организациям: Крису Вайлду (рис. 0.3), Джеймсу Грайму (рис. 2.1), Кэт Мерсер из Natsal (рис. 2.4 и 2.10), Национальной статистической службе Великобритании (рис. 2.9, 8.5 и 9.4), Службе общественного здравоохранения Англии (рис. 6.7), Полу Бардену (рис. 9.2) и «Би-би-си» (рис. 9.3). Общественные данные о Великобритании используются в соответствии с Открытой государственной лицензией, версия 3.0.
