Статистика показала: если забивающий выбирает естественное направление удара, а вратарь двигается в правильную сторону, мяч попадает в ворота в 70 % случаев; если вратарь ошибается, эта цифра вырастает до 90 %. Если забивающий направляет мяч в «неестественный» угол, он попадает в ворота в 60 % случаев при условии, что вратарь предугадает направление удара, и в 95 % при условии ошибки вратаря.
Чтобы свести к минимуму максимальный проигрыш, пенальтист должен бить в естественном направлении; даже если вратарь отреагирует правильно, то есть переместится в нужный угол, шанс на попадание мяча в ворота составит минимум 70 %. Для сравнения: если вратарь совершит ошибку, вероятность гола составит 90 %. Эти данные суммированы в таблице.
Таким образом, если забивающий хочет максимально снизить возможный ущерб, он должен посылать мяч в естественном направлении: даже если вратарь угадает его намерение, шансы забить гол составляют 70 %. Голкипер, в свою очередь, должен падать в сторону, противоположную естественному направлению забивающего. Тогда в наихудшем случае шансы пенальтиста забить гол составят не 95, а 90 %.
Будь такая стратегия оптимальной, вероятность неблагоприятного исхода и для пенальтиста, и для голкипера была бы в процентном соотношении практически одинаковой. Ведь серия пенальти – это игра с нулевой суммой. Каждый ее участник стремится минимизировать потенциальные потери, и если каждый выберет идеальную стратегию, то минимизирует максимальный выигрыш оппонента. Однако говорить об оптимальной стратегии в данном случае не приходится, так как для пенальтиста худший результат – 70-процентная вероятность попадания в ворота, а для вратаря – 90-процентная вероятность пропустить мяч.
Зависимость успешного пенальти от направления удара, выбранного забивающим и вратарем
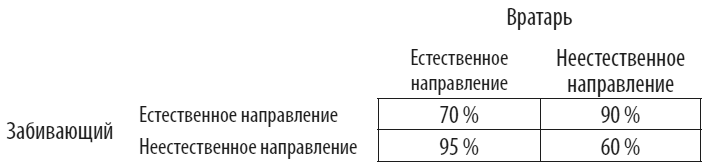
Тот факт, что цифры в столбцах таблицы не равны, подразумевает, что каждый участник может менять свою тактику, пытаясь увеличить шансы на победу. Как и в игре «камень-ножницы-бумага», периодическая смена вектора принесет больше пользы, чем верность чистой стратегии. Например, если пенальтист всегда будет придерживаться естественного направления удара, голкиперу тоже следует иногда выбирать естественное направление, что позволит уменьшить вероятность гола с неблагоприятных 90 до 70 %. Пенальтисту в качестве ответной меры разумно прибегать к смешанной стратегии.
Рассчитывая наилучший алгоритм действий для пенальтиста и голкипера, Паласиос-Хеурта пришел к выводу, что оба должны выбирать естественное направление в 60 % случаев и неестественное – в остальных 40 %. Как и эффективный блеф в покере, это позволит притупить внимание противника и лишить его возможности увеличить свои шансы на победу путем изменения стратегии. Тогда и пенальтист, и голкипер смогут снизить вероятность своей потери, одновременно минимизировав выигрыш противоположной стороны. Примечательно, что рекомендованные 60 % всего лишь на несколько процентов отличаются от частоты, с какой футболисты меняют тактику в реальности. Не значит ли это, что забивающие и вратари – осознанно или нет – уже нашли для себя оптимальную стратегию поведения при пенальти?
Фон Нейман решил проблему минимакса в 1928 году, опубликовав результаты своих исследований в статье «К теории стратегических игр». Доказательство того, что оптимальные стратегии существовали всегда, стало для ученого настоящим открытием. Позже он говорил, что без этих выводов продолжать изучение теории игр было бы бессмысленно.
Метод, при помощи которого фон Нейман разобрался с проблемой минимакса, отличался большой сложностью. Проделанная ученым длительная и многотрудная работа вполне подходит под определение «математического высшего пилотажа». Однако впечатлила она не всех. Французский математик Морис Фреше заявил, что расчеты фон Неймана были проделаны ранее (хотя тот об этом и не подозревал), и, применяя их к теории игры, ученый «ломился в открытую дверь».
Фреше ссылался на исследования своего коллеги Эмиля Бореля, который провел их за несколько лет до фон Неймана. Когда в начале 1950-х работы Бореля наконец-то были напечатаны на английском языке, в предисловии к публикации Фреше назвал изобретателем теории игр Бореля. Фон Неймана это привело в ярость, и ученые устроили яростную перепалку на страницах журнала Econometrica.
Их спор пролил свет на два важных аспекта применения математических методов в повседневной жизни. Во-первых, трудно определить подлинного автора теории. Кому следует отдать этот титул – тому, кто изготовил математические «кирпичики», или тому, кто построил из них нечто полезное? Фреше искренне верил, что именно Борель, создатель «кирпичиков», заслужил лавры первооткрывателя, хотя история присудила их фон Нейману.
Во-вторых, важные научные открытия не всегда получают должное признание в своем первоначальном виде. Защищая Бореля, Фреше настаивал на том, что проблема минимакса уже была известна математикам, пусть и в иной форме. Но ее ценность стала очевидной лишь после работы фон Неймана. Как доказал Фергюсон, применив теорию игр в покере, иногда ничем не примечательная с точки зрения научного сообщества идея, будучи помещена в другой контекст, способна принести огромную пользу.
Пока фон Нейман и Фреше метали друг в друга громы и молнии, Джон Нэш заканчивал в Принстоне докторантуру. Выведя равенство Нэша, он смог расширить применение разработок фон Неймана. Если последний рассматривал игру с нулевой суммой с двумя игроками, то Нэш доказал, что оптимальная стратегия достижима в ситуации с множеством игроков и неравномерным выигрышем. Но фанатам покера мало знать, что идеальная стратегия существует. Это лишь начало большого пути. Следующий шаг – найти ее.
Большинство специалистов, пишущих программы для игры в покер, не обременяют себя изучением теории игр для поиска оптимальной стратегии. Чаще всего они берут за основу набор строгих правил и создают для каждой потенциально возможной ситуации последовательность инструкций типа: «Если случится это – поступай так». Поэтому поведение бота зависит от стиля игры его создателя и от того, как последний представляет себе действия хорошего игрока.
В 2003 году, обучаясь в магистратуре, программист Роберт Фоллек создал покерного бота SoarBot. Программа использовала когнитивную архитектуру Soar, разработанную учеными из Мичиганского университета. Во время игры в покер SoarBot действовал в три этапа. Сначала он сканировал текущую ситуацию – карманные карты, прикуп и количество игроков, сделавших пас. Проанализировав полученную информацию, бот соотносил ее с заложенными в него инструкциями и определял, какие из них применимы к имеющимся обстоятельствам.
Суммировав все возможные варианты действий, программа переходила к этапу принятия решения, делая выбор на основе заложенных в нее Фоллеком параметров. Но здесь возникали проблемы. Иногда имеющихся параметров было недостаточно, и программа либо не находила нужного решения, либо металась между двумя его вариантами. Да и сами параметры часто бывали сомнительны. Поскольку каждый из них Фоллек вводил индивидуально, иногда программа сталкивалась с двумя противоречащими друг другу указаниями. Например, один параметр велел SoarBot делать ставку, а другой требовал сбросить карты.



