Вам предстоит познакомиться с множеством инструментов, но не переживайте — мы начнем с простых задач, а затем по мере изучения новых методов постепенно будем находить все лучшие решения. Достаточно скоро вы научитесь просто и изящно справляться с вычислительными задачами.
3.1. Итерация
Итеративная стратегия состоит в использовании циклов (например, for и while) для повторения процесса до тех пор, пока не окажется соблюдено некое условие. Каждый шаг в цикле называется итерацией. Итерации очень полезны для пошагового просмотра входных данных и применения одних и тех же операций к каждой их порции. Вот пример.
Объединение списков рыб
У вас есть списки морских и пресноводных рыб, оба упорядочены в алфавитном порядке. Как создать из них один общий список, тоже отсортированный по алфавиту?
Мы можем сравнивать в цикле верхние элементы двух списков (рис. 3.1).
Данный процесс можно записать в виде одного цикла с условием продолжения while loop:
function merge(sea, fresh)
····result ← List.new
····while not (sea.empty and fresh.empty)
········if sea.top_item > fresh.top_item
············fish ← sea.remove_top_item
·······else
···········fish ← fresh.remove_top_item
·····result.append(fish)
return result
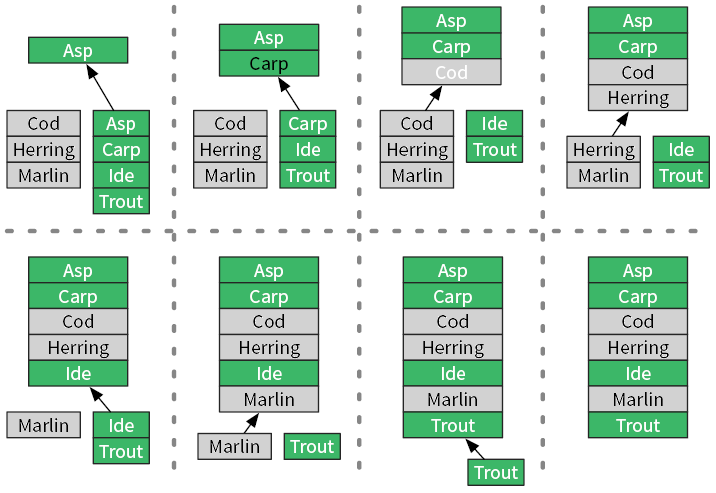
Рис. 3.1. Объединение двух отсортированных списков в третий, тоже отсортированный
Он выполняет обход всех названий рыб из входных списков, совершая фиксированное число операций для каждого элемента
[28]. Следовательно, алгоритм слияния merge имеет сложность O(n).
Вложенные циклы и степенные множества
В предыдущей главе мы увидели, как функция сортировки выбором selection_sort использует один цикл, вложенный в другой. Сейчас мы научимся использовать вложенный цикл для вычисления степенного множества. Если дана коллекция объектов S, то степенное множество S есть множество, содержащее все подмножества S
[29].
Исследование запахов
В парфюмерии цветочные ароматы изготавливают путем комбинирования запахов различных цветов. Если дано множество цветов F, то как посчитать все ароматы, которые можно изготовить из них?
Любой аромат состоит из подмножества F, потому его степенное множество содержит все возможные ароматы. Это степенное множество вычисляется итеративно. Для нулевого множества цветов есть всего один вариант — без запаха. В случае, когда мы берем очередной цветок, мы дублируем уже имеющиеся ароматы и добавляем его к ним (рис. 3.2).
Этот процесс можно описать при помощи циклов. Во внешнем цикле мы принимаем решение, какой цветок будем рассматривать следующим. Внутренний цикл дублирует ароматы и добавляет новый цветок к этим копиям.
function power_set(flowers)
····fragrances ← Set.new
····fragrances.add(Set.new)
····for each flower in flowers
········new_fragrances ← copy(fragrances)
········for each fragrance in new_fragrances
············fragrance.add(flower)
········fragrances ← fragrances + new_fragrances
····return fragrances
Добавление каждого нового цветка приводит к удвоению количества ароматов в множестве fragrances, что говорит об экспоненциальном росте (2k+1 = 2 × 2k). Алгоритмы, которые удваивают число операций, если объем входных данных увеличивается на один элемент, — экспоненциальные, их временная сложность — O(2n).
Генерирование степенных множеств эквивалентно генерированию таблиц истинности (см. раздел «Логика» в главе 1). Если обозначить каждый цветок логической переменной, то любой аромат легко представить в виде значений True/False этих переменных. В таблице истинности каждая строка будет возможной формулой аромата.
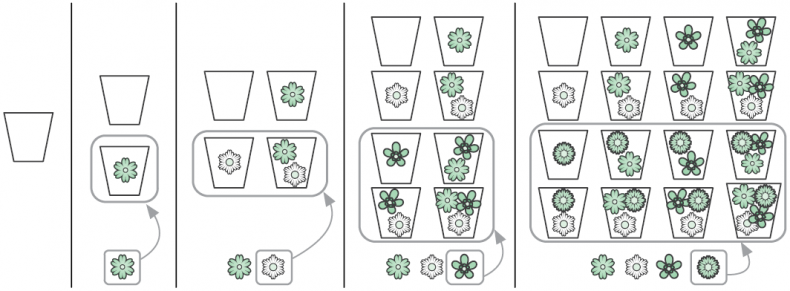
Рис. 3.2. Итеративное перечисление всех ароматов с использованием четырех цветков
3.2. Рекурсия
Мы говорим о рекурсии, когда функция делегирует работу своим клонам. Рекурсивный алгоритм естественным образом приходит на ум, когда нужно решить задачу, сформулированную с точки зрения самой себя. Например, возьмем известную последовательность Фибоначчи. Она начинается с двух единиц, и каждое последующее число является суммой двух предыдущих: 1, 1, 2, 3, 5, 8, 13, 21. Как создать функцию, возвращающую n-е число Фибоначчи (рис. 3.3)?
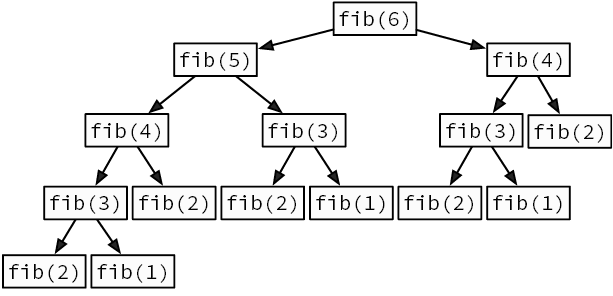
Рис. 3.3. Рекурсивное вычисление шестого числа Фибоначчи
function fib(n)
····if n ≤ 2
