····for each candidate in power_set(items)
········if total_weight(candidate) ≤ max_weight
············if sales_value(candidate) > best_value
················best_value ← sales_value(candidate)
················best_candidate ← candidate
····return best_candidate
Для n предметов существует 2n подборок. В случае каждой из них мы проверяем, не превышает ли ее общий вес вместимости рюкзака и не оказывается ли общая стоимость подборки выше, чем у лучшей, найденной к этому времени. Иными словами, для каждой подборки выполняется постоянное число операций, а значит, алгоритм имеет сложность O(2n).
Однако проверять следует не каждую подборку предметов. Многие из них оставляют рюкзак полупустым, а это указывает на то, что существуют более удачные варианты
[34]. Далее мы узнаем стратегии, которые помогут оптимизировать поиск решения, эффективным образом отбраковывая неподходящие варианты.
3.4. Поиск (перебор) с возвратом
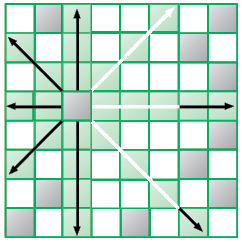
Вы играете в шахматы? Фигуры перемещаются на доске 8 × 8 клеток и поражают фигуры соперника. Ферзь — это самая сильная фигура: она поражает клетки по горизонтали, по вертикали и по двум диагоналям. Следующая стратегия будет объяснена в контексте известной шахматной задачи.
Задача о восьми ферзях
Как разместить восемь ферзей на доске так, чтобы ни один из них не оказался под ударом других?
Попробуйте найти решение вручную, и вы увидите, что оно далеко не тривиальное. Рис. 3.6 показывает один из способов расположения мирно сосуществующих ферзей.
В разделе 1.3 мы видели, что восемь ферзей можно разместить на шахматной доске более чем 4 млрд способами. Решение искать ответ полным перебором, проверяя все варианты, я бы назвал неосмотрительным. Предположим, что первые два ферзя помещены на доску таким образом, что представляют угрозу друг для друга. Тогда независимо от того, где окажутся следующие ферзи, решение найти не удастся. Подход на основе полного перебора не учитывает этого и будет впустую тратить время, пытаясь разместить всех обреченных ферзей.
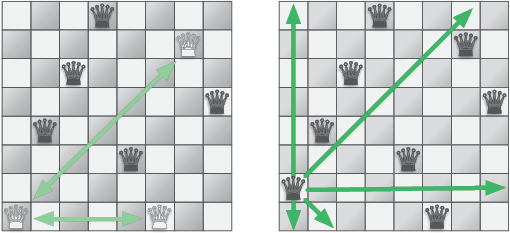
Рис. 3.6. Крайний левый ферзь может бить двух других. Если переместить его на одну клетку вверх, то он не будет никому угрожать
Более эффективный поход состоит в поиске только приемлемых позиций для фигур. Первого ферзя можно поместить куда угодно. Приемлемые позиции для каждого следующего будут ограничены уже размещенными фигурами: нельзя ставить ферзя на клетку, находящуюся под ударом другого ферзя. Если мы начнем руководствоваться этим правилом, мы, вероятно, получим доску, где невозможно разместить дополнительного ферзя, еще до того, как число фигур дойдет до восьми (рис. 3.7).
Это будет означать, что последнего ферзя мы разместили неправильно. Потому нам придется отойти назад — вернуться к предыдущей позиции и продолжить поиск. В этом заключается суть стратегии поиска с возвратом: продолжать размещать ферзей в допустимые позиции. Как только мы окажемся в тупике, мы отойдем назад, к моменту, предшествовавшему размещению последнего ферзя. Этот процесс можно оптимизировать при помощи рекурсии:
function queens(board)
····if board.has_8_queens
········return board
····for each position in board.unattacked_positions
········board.place_queen(position)
········solution ← queens(board)
········if solution
············return solution
········board.remove_queen(position)
····return False
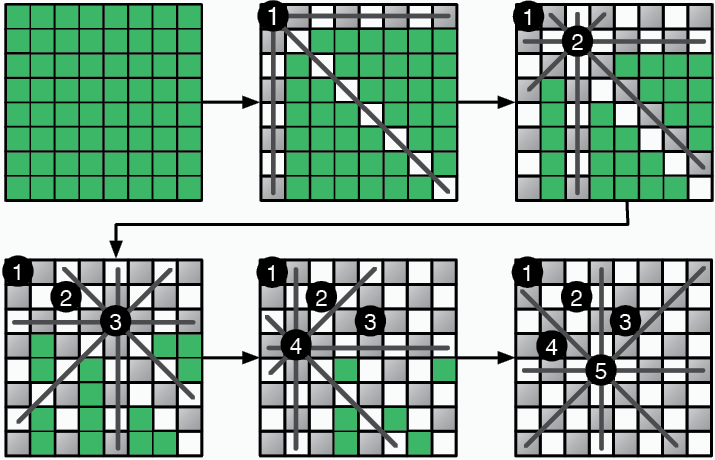
Рис. 3.7. Размещение ферзей ограничивает число приемлемых клеток для следующих фигур
Если требуемое по условию сочетание позиций на доске еще не найдено, функция обходит все приемлемые позиции для следующего ферзя. Она использует рекурсию, чтобы проверить, даст ли размещение ферзя в каждой из этих позиций решение. Как работает процесс, показано на рис. 3.8.
Поиск с возвратом лучше всего подходит для задач, где решением является последовательность вариантов, и выбор одного из них ограничивает выбор последующих. Этот подход позволяет выявлять варианты, которые не дают желаемого решения, так что вы можете отступить и попробовать что-то еще. Ошибитесь как можно раньше, чтобы двигаться дальше.
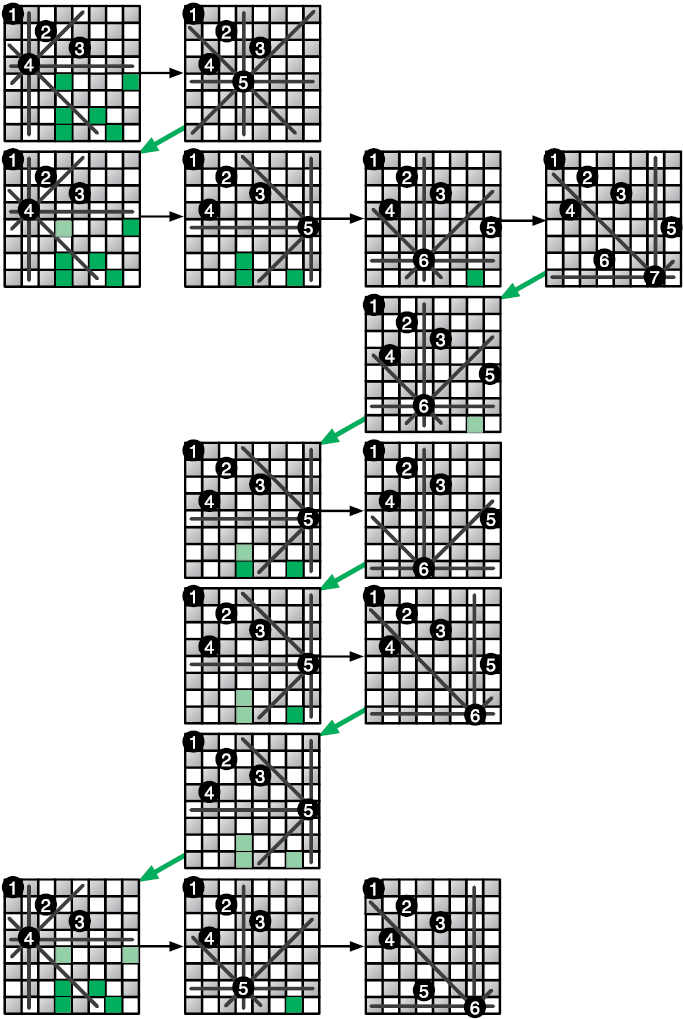
Рис. 3.8. Поиск с возвратом в «Задаче о восьми ферзях»
3.5. Эвристические алгоритмы
В обычных шахматах — 32 фигуры шести типов и 64 клетки, по которым они ходят. После каких-то четырех первых ходов число возможных дальнейших позиций достигает 288 млрд. Даже самые сильные игроки в мире не в состоянии найти идеальный ход. Они полагаются на интуицию, чтобы найти тот, который окажется достаточно хорошим. Мы можем делать то же самое при помощи алгоритмов. Эвристический метод, или просто эвристика, — это метод, который приводит к решению, не гарантируя, что оно — лучшее или оптимальное. Эвристические алгоритмы помогут, когда методы вроде полного перебора или поиска с возвратом оказываются слишком медленными. Существует много отличных эвристических подходов, но мы сосредоточимся на самом простом: на поиске без возврата.
