«Жадные» алгоритмы
Очень распространенный эвристический подход к решению задач — использование так называемых «жадных» алгоритмов. Основная их идея состоит в том, чтобы никогда не откатываться к предыдущим вариантам. Это полная противоположность поиску с возвратом. Иными словами, на каждом шаге мы пытаемся сделать самый лучший выбор, а потом уже не подвергаем его сомнению. Давайте испытаем эту стратегию, чтобы по-новому решить задачу о рюкзаке (из раздела «Полный перебор»
).
Жадный грабитель и рюкзак
Грабитель пробирается в ваш дом, чтобы украсть предметы, которые вы хотели продать. Он решает использовать ваш рюкзак, чтобы унести в нем украденное. Что он возьмет? Имейте в виду, что чем быстрее он уйдет, тем меньше вероятность, что его поймают с поличным.
В сущности, оптимальное решение здесь должно быть ровно таким же, что и в задаче о рюкзаке. Однако у грабителя нет времени для перебора всех комбинаций упаковки рюкзака, ему некогда постоянно откатываться назад и вынимать уже уложенные в рюкзак вещи! Жадина будет совать в рюкзак самые дорогие предметы, пока не заполнит его:
function greedy_knapsack(items, max_weight)
····bag_weight ← 0
····bag_items ← List.new
····for each item in sort_by_value(items)
········if max_weight ≤ bag_weight + item.weight
············bag_weight ← bag_weight + item.weight
············bag_items.append(item)
····return bag_items
Здесь мы не принимаем во внимание то, как наше текущее действие повлияет на будущие варианты выбора. Такой «жадный» подход позволяет отыскать подборку предметов намного быстрее, чем метод полного перебора. Однако он не дает никакой гарантии, что общая стоимость подборки окажется максимальной.
В вычислительном мышлении жадность — это не только смертный грех. Будучи добропорядочным торговцем, вы, возможно, тоже испытываете желание напихать в рюкзак всего побольше или очертя голову отправиться в поездку.
Снова коммивояжер
Коммивояжер должен посетить n заданных городов и закончить маршрут в той точке, откуда он его начинал. Какой план поездки позволит минимизировать общее пройденное расстояние?
Как мы убедились в разделе «Комбинаторика» (см. главу 1), число возможных комбинаций в этой задаче демонстрирует взрывной рост и достигает неприлично больших величин, даже если городов всего несколько. Найти оптимальное решение задачи коммивояжера с тысячами городов — чрезвычайно дорого (а то и вовсе невозможно)
[35]. И тем не менее вам нужен маршрут. Вот простой «жадный» алгоритм для этой задачи:
1) посетить ближайший город, где вы еще не были;
2) повторять, пока не объедете все города.
Рис. 3.9. Задача коммивояжера
[36]
Можете ли вы придумать более хороший эвристический алгоритм, чем тот, что использует «жадный» подход? Специалисты по информатике вовсю ломают голову над этим вопросом.
Когда жадность побеждает силу
Выбирая эвристический алгоритм вместо классического, вы идете на компромисс. Насколько далеко от идеального решения вы можете отойти, чтобы результат все еще удовлетворял вас? Это зависит от конкретной ситуации.
Впрочем, даже если вам непременно требуется найти идеальный вариант, не стоит сбрасывать эвристику со счетов. Эвристический подход иногда приводит к самому лучшему решению. Например, вы можете разработать «жадный» алгоритм, способный найти такое же решение, что и алгоритм полного перебора. Давайте посмотрим, как такое осуществляется.
Электрическая сеть
Поселки в удаленном районе не были электрифицированы, но вот в одном из них начали строить электростанции. Энергия пойдет от поселка к поселку по линиям электропередач. Как включить все поселки в сеть, используя минимум проводов?
Данная задача может быть решена очень просто.
1. Среди поселков, еще не подключенных к сети, выбрать тот, который находится ближе всех к электрифицированному поселку, и соединить их.
2. Повторять, пока все поселки не будут подключены.
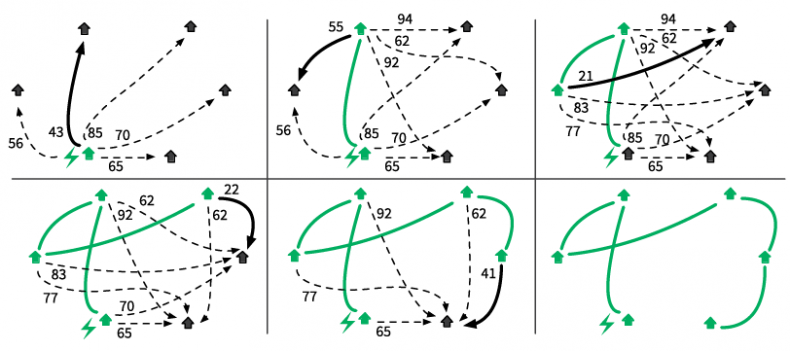
Рис. 3.10. Решение задачи об электрической сети с «жадными» вариантами выбора
На каждом шаге мы выбираем для соединения пару поселков, которая на текущий момент выглядит самой лучшей. Несмотря на то что мы не анализируем, как этот вариант влияет на будущие возможности выбора, присоединение самого близкого поселка без электричества — всегда правильный выбор. Здесь нам повезло: структура задачи идеально подходит для решения «жадным» алгоритмом. В следующем разделе мы увидим структуры задач, для решения которых нужна стратегия великих полководцев.
3.6. Разделяй и властвуй
Когда силы врага раздроблены на небольшие группы, его проще победить. Цезарь и Наполеон управляли Европой, разделяя и завоевывая своих врагов. При помощи той же стратегии вы можете решать задачи — в особенности задачи с оптимальной подструктурой, то есть такие, которые легко делятся на подобные, но меньшие подзадачи. Их можно дробить снова и снова, пока подзадачи не станут простыми. Затем их решения объединяются — так вы получаете решение исходной задачи.
