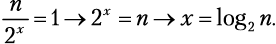Разделить и отсортировать
Если у нас есть большой список, который нужно отсортировать, мы можем разделить его пополам: каждая половина становится подзадачей сортировки. Затем решения подзадач (то есть отсортированные половины списка) можно объединить в конечное решение при помощи алгоритма слияния
[37]. Но как отсортировать эти две половины? Их тоже можно разбить на подзадачи, отсортировать и объединить.
Новые подзадачи будут также разбиты, отсортированы и объединены. Процесс разделения продолжаем, пока не достигнем базового случая: списка из одного элемента. Такой список уже отсортирован!
Этот изящный рекурсивный алгоритм называется сортировкой слиянием. Как и для последовательности Фибоначчи (см. раздел «Рекурсия»), дерево рекурсивных вызовов помогает увидеть, сколько раз функция merge_sort вызывает саму себя (рис. 3.11).
function merge_sort(list)
····if list.length = 1
········return list
····left ← list.first_half
····right ← list.last_half
····return merge(merge_sort(left),
·················merge_sort(right))
Теперь давайте найдем временную сложность сортировки слиянием. Для этого сначала подсчитаем операции, выполняемые на каждом отдельном шаге разбиения, а затем — общее количество шагов.
Подсчет операций. Допустим, у нас есть большой список размером n. При вызове функция merge_sort выполняет следующие операции:
• разбивает список на половины, что не зависит от размера списка O(1);
• вызывает функцию merge (из раздела «Итерация» мы знаем, что merge имеет сложность O(n);
• делает два рекурсивных вызова merge_sort, которые не учитываются
[38].
Поскольку мы оставляем только доминирующий член и не учитываем рекурсивные вызовы, временная сложность функции составляет O(n). Теперь подсчитаем временную сложность каждого шага разбиения.
Шаг разбиения 1. Функция merge_sort вызывается для списка из n элементов. Временная сложность этого шага составляет O(n).
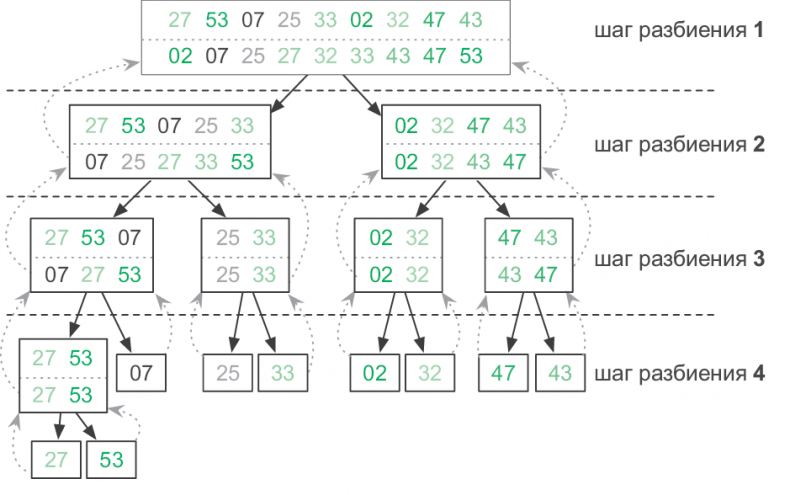
Рис. 3.11. Демонстрация сортировки слиянием. Прямоугольники показывают отдельные вызовы merge_sort, при этом входные данные находятся вверху, а выходные — внизу
Шаг разбиения 2. Функция merge_sort вызывается дважды, каждый раз для
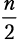 элементов. Мы получаем
элементов. Мы получаем
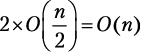 .
.
Шаг разбиения 3. Функция merge_sort вызывается четыре раза, каждый раз для
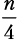 элементов:
элементов:
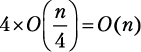 .
.
.
.
.
.
Шаг разбиения x. Функция merge_sort вызывается 2x раз, каждый для списка из
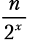 элементов:
элементов:
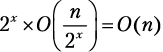 .
.
Все шаги разбиения имеют одинаковую сложность O(n). Временная сложность сортировки слиянием, следовательно, составляет x × O(n), где x — это количество шагов разбиения, необходимых для полного выполнения алгоритма
[39].
Подсчет шагов. Как вычислить x? Мы знаем, что рекурсивные функции заканчивают вызывать себя, как только достигают своего базового случая. Наш базовый случай — это одноэлементный список. Мы также увидели, что шаг разбиения x работает на списках из
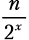 элементов. Потому:
элементов. Потому:
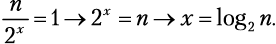
Если вы не знакомы с функцией log2, то не робейте! x = log2 n — это просто еще один способ написать 2x = n. Программисты любят логарифмический рост.
Посмотрите, как медленно растет количество требуемых шагов разбиения
[40] с увеличением общего числа сортируемых элементов (табл. 3.1).




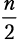 элементов. Мы получаем
элементов. Мы получаем
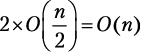 .
.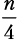 элементов:
элементов:
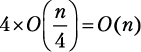 .
.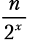 элементов:
элементов:
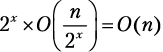 .
.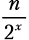 элементов. Потому:
элементов. Потому: