День с самой низкой ценой перед днем 3, но не в день 3 — это B(2). Потому для B(3):
• P(3) < цена в день B(2) —> B(3) = 3.
• P(3) ≥ цена в день B(2) —> B(3) = B(2).
Обратите внимание, что день с самой низкой ценой перед днем 4 будет B(3). Фактически для каждого n день с самой низкой ценой перед днем n — B(n — 1). Мы можем это использовать, чтобы выразить B(n) через B(n — 1):
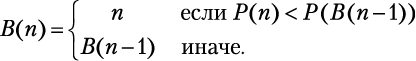
Когда у нас есть все пары [n, B(n)] для для каждого дня n, решением является пара, которая дает самую высокую прибыль. Следующий алгоритм решает задачу, вычисляя все значения B снизу вверх:
function trade_dp(P)
····B[1] ← 1
····sell_day ← 1
····best_profit ← 0
····for each n from 2 to P.length
········if P[n] < P[B[n-1]]
············B[n] ← n
········else
············B[n] ← B[n-1]
········profit ← P[n] — P[B[n]]
········if profit > best_profit
············sell_day ← n
············best_profit ← profit
····return (sell_day, B[sell_day])
Алгоритм выполняет фиксированное число простых операций для каждого элемента входного списка, следовательно, он имеет сложность O(n). Это огромный рывок в производительности по сравнению со сложностью предыдущего алгоритма O(n log n) — и совершенно несравнимо со сложностью O(n2) метода полного перебора. Этот алгоритм также имеет пространственную сложность O(n), поскольку вспомогательный вектор B содержит столько же элементов, что и входные данные. Из приложения IV вы узнаете, как сэкономить память за счет создания алгоритма с пространственной сложностью O(1).
3.8. Ветви и границы
Многие задачи связаны с минимизацией или максимизацией целевого значения: найти кратчайший путь, получить наибольшую прибыль и т. д. Такие задачи называются задачами оптимизации. Когда решением является последовательность вариантов, мы часто используем стратегию ветвей и границ. Ее цель состоит в том, чтобы выиграть время за счет быстрого обнаружения и отбрасывания плохих вариантов. Чтобы понять, каким образом они ищутся, мы сначала должны разобраться в понятиях «верхняя граница» и «нижняя граница».
Верхние и нижние границы
Границы обозначают диапазон значения. Верхняя граница устанавливает предел того, каким высоким оно может быть. Нижняя граница — это наименьшее значение, на которое стоит надеяться; она гарантирует, что любое значение либо равно ей, либо ее превышает.
Мы порой легко находим решения, близкие к оптимальным: короткий путь — но, возможно, не самый короткий; большая прибыль — но, возможно, не максимальная. Они дают границы оптимального решения. К примеру, любой короткий маршрут из одной точки в другую никогда не будет короче расстояния между ними по прямой. Следовательно, расстояние по прямой является нижней границей самого короткого пути.
В задаче о жадном грабителе и рюкзаке (см. раздел «Эвристические алгоритмы»
) прибыль, полученная посредством greedy_knapsack, является нижней границей оптимальной прибыли (она может быть или не быть близкой к оптимальной прибыли). Теперь представим версию задачи о рюкзаке, в которой вместо предметов у нас сыпучие материалы, и мы можем насыпать их в рюкзак, сколько поместится. Эта версия задачи решается «жадным» способом: просто продолжайте насыпать материалы с самым высоким соотношением стоимости и веса:
function powdered_knapsack(items, max_weight)
····bag_weight ← 0
····bag_items ← List.new
····items ← sort_by_value_weight_ratio(items)
····for each i in items
········weight ← min(max_weight — bag_weight,
·····················i.weight)
········bag_weight ← bag_weight + weight
········value ← weight * i.value_weight_ratio
········bagged_value ← bagged_value + value
········bag_items.append(item, weight)
····return bag_items, bag_value
Добавление ограничения неделимости предметов только уменьшит максимально возможную прибыль, потому что нам придется менять последнюю уложенную в рюкзак вещь на что-то подешевле. Это означает, что powdered_knapsack дает верхнюю границу оптимальной прибыли с неделимыми предметами
[43].
Ветви и границы в задаче о рюкзаке
Мы уже убедились, что поиск оптимальной прибыли в задаче о рюкзаке требует дорогих вычислений O(n2). Однако мы можем быстро получить верхние и нижние границы оптимальной прибыли при помощи функций powdered_knapsack и greedy_knapsack. Давайте попробуем это сделать на примере задачи о рюкзаке (табл. 3.3).
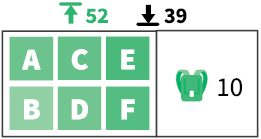
Таблица 3.3. Верхняя и нижняя границы в задаче о рюкзаке
| Предмет |
Стоимость |
Вес |
Соотношение стоимости и веса |
Макс. вместимость |
| A |
20 |
5 |
4,00 |
|
| B |
19 |
4 |
4,75 |
|
| C |
16 |
2 |
8,00 |
10 |
| D |
14 |
5 |
2,80 |
|
| E |
13 |
3 |
4,33 |
|
| F |
9 |
2 |
4,50 |
|
