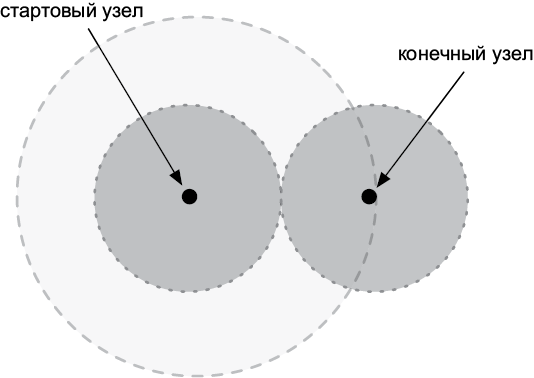
Рис. 5.4. Пространства однонаправленного и двунаправленного поиска
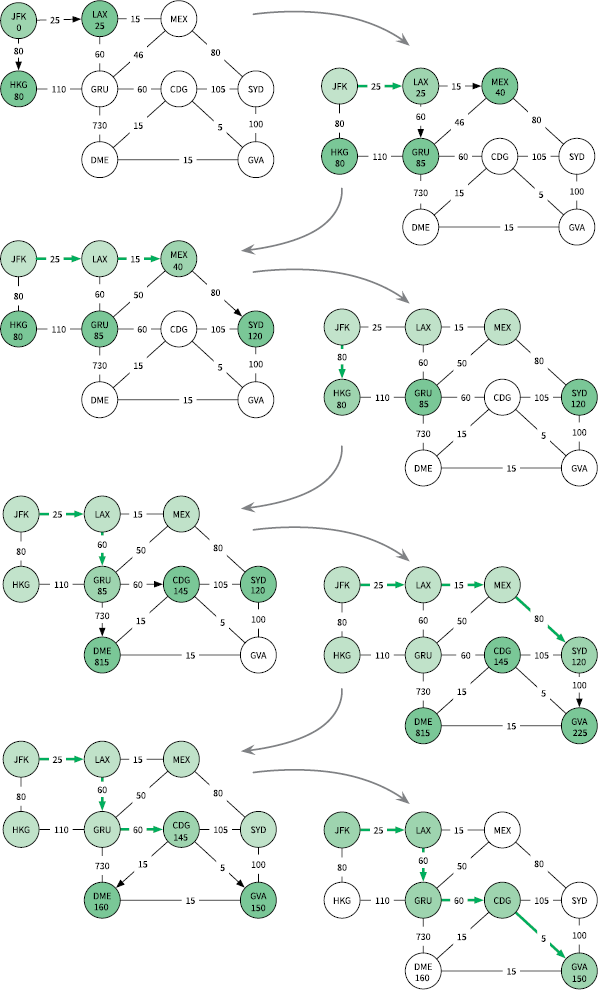
Рис. 5.5. Поиск кратчайшего маршрута от аэропорта JFK до аэропорта GVA при помощи алгоритма Дейкстры
PageRank
Вы когда-нибудь задавались вопросом, как поисковой системе Google удается анализировать миллиарды веб-страниц и показывать вам самые подходящие? В этом процессе задействовано множество алгоритмов, но самым важным является алгоритм PageRank.
Прежде чем основать компанию Google, Сергей Брин и Ларри Пейдж работали научными сотрудниками в области computer science в Стэнфордском университете и занимались исследованием графовых алгоритмов. Они смоделировали Всемирную паутину в виде графа: веб-страницы — это вершины, и связи между ними — ребра.
Они решили, что если веб-страница получает много связей от других важных страниц, то она тоже должна быть важной. Опираясь на эту идею, они создали алгоритм PageRank. Он выполняется в несколько заходов. Вначале каждая веб-страница в графе имеет то же количество единиц значимости, что и остальные. После каждого захода она распределяет свои единицы среди страниц, ссылки на которые на ней размещены. Этот процесс повторяется до тех пор, пока все значения не стабилизируются. Стабилизированная оценка каждой страницы называется ее рангом, отсюда и название — PageRank (англ. «ранг страницы»). Используя этот алгоритм для определения важности веб-страниц, поисковая система Google быстро заняла доминирующую позицию среди других аналогичных сервисов.
Алгоритм PageRank применим и к другим типам графов. Например, мы можем смоделировать пользователей сети Twitter на графе, а затем вычислить ранг каждого. Как вы считаете, будут ли пользователи с более высоким рангом известными людьми?
5.4. Исследование операций
Во время Второй мировой войны британская армия столкнулась с необходимостью оптимизировать принятие стратегических решений, чтобы повысить действенность операций. Было разработано большое количество аналитических инструментов для выявления наилучшего способа координации военных действий.
Эта практическая дисциплина получила название исследование операций. Она позволила усовершенствовать британскую систему радаров дальнего обнаружения и помогла Соединенному Королевству лучше управлять людскими и материальными ресурсами. Во время войны сотни британцев участвовали в исследовании операций. В дальнейшем для оптимизации процессов в торгово-промышленной деятельности были применены новые идеи. Исследование операций включает в себя определение целевого показателя, который подлежит оптимизации, то есть максимизации или минимизации. Эта дисциплина позволяет максимизировать такие целевые показатели, как урожай, прибыль или производительность, и минимизировать убытки, риск или стоимость.
Например, исследование операций используется авиакомпаниями для оптимизации графиков полетов. Точные корректировки в планировании распределения трудовых ресурсов и оборудования могут сэкономить миллионы долларов. Еще один пример касается нефтеперерабатывающих заводов, где определение оптимальных пропорций сырья в смеси может рассматриваться как задача исследования операций.
Задачи линейной оптимизации
Задачи, где целевой показатель и ограничения можно смоделировать с использованием линейных уравнений
[55], называются задачами линейной оптимизации. Давайте посмотрим, как решаются эти задачи.
Умная меблировка
В вашем офисе не хватает каталожных шкафов. Шкаф X стоит 10 долларов, занимает 6 квадратных футов и содержит 8 кубических футов папок. Шкаф Y стоит 20 долларов, занимает 8 квадратных футов и содержит 12 кубических футов папок. У вас есть 140 долларов, и вы можете использовать под шкафы до 72 квадратных футов площади офиса. Какие шкафы следует приобрести, чтобы максимизировать емкость хранения?
Прежде всего определим переменные нашей задачи. Мы хотим найти количество шкафов каждого типа, которые следует приобрести, поэтому:
• x — количество шкафов модели X;
• y — количество шкафов модели Y.
Мы хотим максимизировать емкость хранения. Дадим емкости хранения имя z и смоделируем это значение как функцию от x и y:
• z = 8x + 12y.
Теперь выберем значения x и y, которые дадут максимальное значение z. При этом мы должны соблюсти ограничение по бюджету (то есть уложиться в 140 долларов) и по площади (она должна быть меньше 72 квадратных футов). Смоделируем эти ограничения:
• 10x + 20y ≤ 140 (ограничение по бюджету);
• 6x + 8y ≤ 72 (ограничение по площади);
• x ≥ 0, y ≥ 0 (нельзя купить отрицательное количество шкафов).
Как бы вы решили эту задачу? Покупка максимального количества шкафов с наилучшим соотношением хранение/площадь не является правильным решением, потому что пространство под установку шкафов ограниченно. Можно пойти по пути полного перебора: написать программу, вычисляющую z для всех возможных x и y, и получить пару, дающую оптимальное z. Это решение годится для простых задач, но оно невыполнимо при большом количестве переменных.
Оказывается, что решать задачи линейной оптимизации вроде этой можно и без программирования. Нужно просто использовать правильный инструмент для работы: симплекс-метод. Он очень эффективно справляется с задачами линейной оптимизации. Симплекс-метод помогает целым отраслям решать сложные проблемы, начиная с 1960-х годов. Когда перед вами встанет такая задача, не изобретайте колесо, просто возьмите готовый симплексный решатель.
Симплексные решатели требуют указать функцию для максимизации (или минимизации) и уравнения, моделирующие ограничения. Решатель сделает все остальное. В данной задаче максимальное значение z достигается при x = 8 и y = 3.
