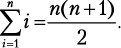
III. Множества
Мы используем слово множество для описания группы объектов. Например, мы можем назвать S множеством обезьянок-эмодзи:
S = {
 ,
,
 ,
,
 ,
,
 }.
}.
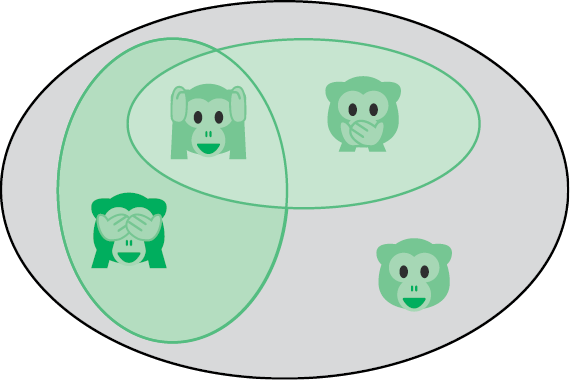
Рис. III.1. S1 и S2 есть подмножества S
Подмножества. Множество объектов, содержащихся в другом множестве, называется подмножеством. Например, обезьянки, показывающие лапы и глаза, составляют подмножество S1 = {
 ,
,
 }. Все обезьянки в S1 содержатся в S. Мы записываем это так: S1
}. Все обезьянки в S1 содержатся в S. Мы записываем это так: S1
 S Мы можем сгруппировать обезьянок с лапками и ртами в другом подмножестве: S2 = {
S Мы можем сгруппировать обезьянок с лапками и ртами в другом подмножестве: S2 = {
 ,
,
 }.
}.
Объединение. Какие обезьянки принадлежат либо S1, либо S2? Ответ: обезьянки в S3 = {
 ,
,
 ,
,
 }. Новое множество — объединение двух предыдущих. Мы записываем это так: S3 = S1
}. Новое множество — объединение двух предыдущих. Мы записываем это так: S3 = S1
 S2.
S2.
Пересечение. Какие обезьянки принадлежат и S1, и S2? Ответ: обезьянки в S4 = {
 }. Новое множество получается путем пересечения двух предыдущих. Мы записываем это так: S4 = S1
}. Новое множество получается путем пересечения двух предыдущих. Мы записываем это так: S4 = S1
 S2.
S2.
Степенные множества. Обратите внимание, что S3 и S4 одновременно являются подмножествами S. Мы также полагаем, что S5 = S и пустое множество S6 = {} являются подмножествами S. Если подсчитать все подмножества S, то вы найдете 24 = 16 подмножеств. Если же рассматривать их все как объекты, то мы можем собрать их в множество. Множество всех подмножеств S называется его степенным множеством:
PS = {S1, S2, S16}.
IV. Алгоритм Кэдейна
В разделе «Полный перебор» главы 3 мы представили задачу «Лучшая сделка».
Лучшая сделка
 У вас есть список цен на золото по дням за какой-то интервал времени. В этом интервале вы хотите найти такие два дня, чтобы, купив золото, а затем продав его, вы получили бы максимально возможную прибыль.
У вас есть список цен на золото по дням за какой-то интервал времени. В этом интервале вы хотите найти такие два дня, чтобы, купив золото, а затем продав его, вы получили бы максимально возможную прибыль.
В разделе «Динамическое программирование» той же главы мы показали алгоритм, который решил эту задачу с временной сложностью O(n) и пространственной сложностью O(n). Когда в 1984 году Джей Кэдейн обнаружил эту задачу, он нашел способ решить ее с O(n) по времени и O(1) по пространству:

