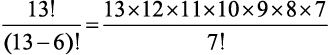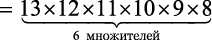1.3. Комбинаторика
Важно уметь считать вещи правильно, ведь в случае с вычислительными задачами вам придется делать это много раз
[16]. Математика далее будет еще более сложной, чем раньше, но не пугайтесь. Кое-кто полагает, что ему не стать хорошим программистом только потому, что, как ему кажется, математик он так себе. Если хотите знать, лично я завалил школьный экзамен по математике
 , и все же я стал тем, кем хотел
, и все же я стал тем, кем хотел
 . В школе дают совсем не ту математику, которая делает людей хорошими программистами.
. В школе дают совсем не ту математику, которая делает людей хорошими программистами.
Никто не захочет зубрить формулы и пошаговые процедуры, если он уже сдал выпускные экзамены. Если такая информация вдруг понадобится — ее легко отыскать в Интернете. Расчеты не обязательно делать от руки на бумаге. От программиста в первую очередь требуется интуиция. Познания в комбинаторике и умение решать комбинаторные задачи развивает эту интуицию. Так что давайте поработаем с несколькими инструментами по порядку: с умножением, перестановками, сочетаниями и суммами.
Правило умножения
Если некоторое событие происходит n разными способами, а другое событие — m разными способами, то число разных способов, которыми могут произойти оба события, равно n × m. Вот пара примеров.
Взлом кода
 Предположим, что PIN-код состоит из двух цифр и латинской буквы. На то, чтобы ввести код один раз, уходит в среднем одна секунда. Какое максимальное время потребуется, чтобы подобрать правильный PIN-код?
Предположим, что PIN-код состоит из двух цифр и латинской буквы. На то, чтобы ввести код один раз, уходит в среднем одна секунда. Какое максимальное время потребуется, чтобы подобрать правильный PIN-код?
Две цифры можно набрать 100 способами (00–99), букву — 26 способами (A — Z). Следовательно, всего существует 100 × 26 = 2600 PIN-кодов. В худшем случае, чтобы подобрать правильный, нам придется перепробовать их все. Через 2600 секунд (то есть через 43 минуты) мы его точно взломаем.
Формирование команды
 Допустим, 23 человека хотят вступить в вашу команду. В отношении каждого кандидата вы подбрасываете монету и принимаете его, только если выпадет «орел». Сколько всего может быть вариантов состава команды?
Допустим, 23 человека хотят вступить в вашу команду. В отношении каждого кандидата вы подбрасываете монету и принимаете его, только если выпадет «орел». Сколько всего может быть вариантов состава команды?
До начала набора есть всего один вариант состава — вы сами. Далее каждый бросок монеты удваивает число возможных вариантов. Это должно быть сделано 23 раза, таким образом, вам нужно посчитать, чему равно 2 в степени:
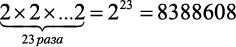 вариантов команды.
вариантов команды.
Обратите внимание, что один из этого множества вариантов — когда в команде состоите только вы.
Перестановки
Если у нас n элементов, то мы можем упорядочить их n! разными способами. Факториал числа имеет взрывной характер, даже с малыми значениями n он дает огромные числа. На случай, если вы с ним не знакомы:
n! = n × (n — 1) × (n — 2) … × 2 × 1.
Легко заметить, что n! — это общее количество способов упорядочивания n элементов. Сколькими способами можно выбрать первый элемент из n? После того как он будет выбран, сколькими способами можно выбрать второй? Сколько вариантов останется для третьего? Подумайте об этом некоторое время, а потом переходите к примерам
[17].
Коммивояжер
 Ваша транспортная компания осуществляет поставки в 15 городов. Вы хотите знать, в каком порядке лучше объезжать эти города, чтобы уменьшить расход топлива. Если на вычисление длины одного маршрута требуется микросекунда, то сколько времени займет вычисление длины всех возможных маршрутов?
Ваша транспортная компания осуществляет поставки в 15 городов. Вы хотите знать, в каком порядке лучше объезжать эти города, чтобы уменьшить расход топлива. Если на вычисление длины одного маршрута требуется микросекунда, то сколько времени займет вычисление длины всех возможных маршрутов?
Любая перестановка 15 городов дает новый маршрут. Факториал — это количество различных комбинаций, так что всего существует 15! = 15 × 14 × … × 1 ≈ 1,3 трлн маршрутов. Число микросекунд, которые уйдут на их вычисление, примерно эквивалентно 15 дням. Будь у вас не 15, а 20 городов, вам бы понадобилось 77 тысяч лет.
Совершенная мелодия
 Девушка разучивает гамму из 13 нот. Она хочет, чтобы вы показали все возможные мелодии, в которых используется 6 нот. Каждая нота должна встречаться один раз на мелодию, а каждая такая мелодия должна звучать в течение одной секунды. О какой продолжительности звучания идет речь?
Девушка разучивает гамму из 13 нот. Она хочет, чтобы вы показали все возможные мелодии, в которых используется 6 нот. Каждая нота должна встречаться один раз на мелодию, а каждая такая мелодия должна звучать в течение одной секунды. О какой продолжительности звучания идет речь?
Мы должны подсчитать количество комбинаций по 6 нот из 13. Чтобы исключить неиспользуемые ноты, нужно остановить вычисление факториала после шестого множителя. Формально
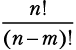 — это количество возможных комбинаций m из n возможных элементов. В нашем случае получится:
— это количество возможных комбинаций m из n возможных элементов. В нашем случае получится:
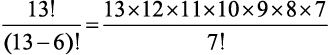
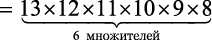
= 1 235 520 мелодий.



 , и все же я стал тем, кем хотел
, и все же я стал тем, кем хотел
 . В школе дают совсем не ту математику, которая делает людей хорошими программистами.
. В школе дают совсем не ту математику, которая делает людей хорошими программистами. Предположим, что PIN-код состоит из двух цифр и латинской буквы. На то, чтобы ввести код один раз, уходит в среднем одна секунда. Какое максимальное время потребуется, чтобы подобрать правильный PIN-код?
Предположим, что PIN-код состоит из двух цифр и латинской буквы. На то, чтобы ввести код один раз, уходит в среднем одна секунда. Какое максимальное время потребуется, чтобы подобрать правильный PIN-код? Допустим, 23 человека хотят вступить в вашу команду. В отношении каждого кандидата вы подбрасываете монету и принимаете его, только если выпадет «орел». Сколько всего может быть вариантов состава команды?
Допустим, 23 человека хотят вступить в вашу команду. В отношении каждого кандидата вы подбрасываете монету и принимаете его, только если выпадет «орел». Сколько всего может быть вариантов состава команды?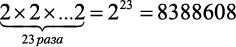 вариантов команды.
вариантов команды. Ваша транспортная компания осуществляет поставки в 15 городов. Вы хотите знать, в каком порядке лучше объезжать эти города, чтобы уменьшить расход топлива. Если на вычисление длины одного маршрута требуется микросекунда, то сколько времени займет вычисление длины всех возможных маршрутов?
Ваша транспортная компания осуществляет поставки в 15 городов. Вы хотите знать, в каком порядке лучше объезжать эти города, чтобы уменьшить расход топлива. Если на вычисление длины одного маршрута требуется микросекунда, то сколько времени займет вычисление длины всех возможных маршрутов? Девушка разучивает гамму из 13 нот. Она хочет, чтобы вы показали все возможные мелодии, в которых используется 6 нот. Каждая нота должна встречаться один раз на мелодию, а каждая такая мелодия должна звучать в течение одной секунды. О какой продолжительности звучания идет речь?
Девушка разучивает гамму из 13 нот. Она хочет, чтобы вы показали все возможные мелодии, в которых используется 6 нот. Каждая нота должна встречаться один раз на мелодию, а каждая такая мелодия должна звучать в течение одной секунды. О какой продолжительности звучания идет речь?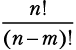 — это количество возможных комбинаций m из n возможных элементов. В нашем случае получится:
— это количество возможных комбинаций m из n возможных элементов. В нашем случае получится: