
Великобритания и Ирландия на фотографии, сделанной 26 марта 2012 года спутником НАСА Terra.
В 1961 году, когда Ричардсон опубликовал результаты своих исследований, мало кто обратил внимание на его удивительное открытие, сейчас называемое эффектом Ричардсона или парадоксом береговой линии. Но теперь оно видится нам важным вкладом в развитие удивительной новой области математики, которую Мандельброт, человек, прославивший ее, в итоге назвал “прекрасной, чертовски трудной и с каждым днем все более ценной”. В 1975 году Мандельброт придумал название для странных штуковин, ставших объектом изучения этой новой дисциплины: фракталы. Фрактал – это нечто (например, кривая или пространство), имеющее дробную размерность.
Чтобы заслужить звание фрактала, фигуре нужно всего лишь иметь сложную структуру в любом масштабе, сколь бы крупным он ни был. Подавляющее большинство кривых и геометрических фигур в математике – не фракталы. Окружность, например, нельзя считать фракталом потому, что, если постепенно увеличивать часть составляющей ее кривой, она будет все больше и больше походить на прямую линию, после чего, сколько ее ни приближай, ничего нового уже не увидишь. Квадрат – тоже не фрактал. При увеличении его углы не меняют свою структуру, а все остальное выглядит как прямые линии. Чтобы быть фракталом, мало иметь сложную структуру в одной точке или даже во множестве (конечном множестве) точек; структура должна быть сложной во всех точках. То же касается и трехмерных фигур, и фигур более высоких размерностей. Сферы и кубы, например, – не фракталы. Но существует множество фигур различных размерностей, которые являются фракталами.
Вернемся к береговой линии Великобритании. На карте малого масштаба показаны только самые крупные заливы, лагуны и полуострова. Но выйдите на пляж – и вы увидите более мелкие объекты: бухты, косы и так далее. Всмотритесь пристальнее, возьмите лупу или микроскоп, и вы различите совсем неприметные элементы – неровности каждого валуна на берегу. И так все дальше и дальше. В реальном мире приближать объект бесконечно невозможно. На уровне атомов и молекул (а возможно, и раньше) уже нет смысла говорить о более мелких деталях, влияющих на длину побережья, тем более что эта длина меняется каждую минуту из-за эрозии, отливов и приливов. И все же побережье Великобритании и очертания других островов и стран – достаточно близкий аналог фракталов, что объясняет, почему могут так различаться данные разных источников о длине пограничной линии. Глядя на карту Великобритании, не увидишь всей изрезанности побережья, которая становится очевидной, когда идешь по берегу пешком. Вот почему измеренная по карте береговая линия получается короче. А простая прогулка по пляжу не даст столь же точных результатов, как измерение линейкой или еще более прецизионным инструментом всех изгибов и неровностей каменистого берега, обводов валунов и прочих мелких деталей. При этом с увеличением точности измерений длина береговой линии возрастает экспоненциально, вместо того чтобы приближаться к некоему конечному “истинному” значению. Другими словами, при наличии измерительного оборудования с достаточно высокой разрешающей способностью вы можете получить любую, сколь угодно большую, длину береговой линии (разумеется, в тех пределах, что устанавливает атомная природа вещества).
Помимо естественных фракталов, таких как контуры побережья, существует и множество фракталов чисто математических. Простой способ изобразить фрактал – разделить отрезок прямой на три равных части, затем, используя среднюю часть как основание, построить на ней равносторонний треугольник, а потом его основание стереть. После этого процесс повторить на каждом из получившихся четырех отрезков, затем на каждом из новых коротеньких отрезков – и так далее, пока не надоест или до бесконечности. Окончательный результат носит название кривой Коха, в честь шведского математика Хельге фон Коха, посвятившего ей опубликованную в 1904 году научную статью. Три кривых Коха можно объединить в фигуру, известную как снежинка Коха
[15]. Кривая Коха стала одной из первых построенных человеком фрактальных фигур. Еще два хорошо известных сегодня фрактала были математически описаны в первой четверти XX века польским математиком Вацлавом Серпинским и носят его имя: треугольник (или салфетка) и ковер Серпинского. Чтобы получить салфетку, Серпинский разделил равносторонний треугольник на четыре новых, с длиной стороны в два раза меньшей, чем у исходного. Затем он удалил центральный и повторил процедуру с каждым из оставшихся трех равносторонних треугольников, потом с получившимися новыми и так далее. Хотя всерьез математики начали изучать такие объекты около столетия назад, художники знали о них еще с античных времен. Салфетку Серпинского, например, можно увидеть на произведениях итальянских мастеров (например, на мозаике собора в городе Ананьи), датируемых еще XIII веком.
Одна из наиболее интересных и парадоксальных черт фракталов – их размерность. Слово “размерность” обычно вызывает две ассоциации: первая – это размеры какого-либо объекта, вторая – некое направление в пространстве, одно из измерений, о которых мы говорили во второй главе. Мы говорим о кубе, что он имеет размерность 3, поскольку его грани лежат в плоскостях, простирающихся в трех разных направлениях под прямыми углами друг к другу. Это второе, интуитивное, понимание размерности – количество перпендикулярных направлений, в которых можно передвигаться, – приблизительно соответствует тому, что в математике называется топологической размерностью. Сфера имеет топологическую размерность 2, потому что мы можем передвигаться по ней в направлениях, обозначаемых как север и юг или восток и запад. А вот шар имеет топологическую размерность 3, поскольку у него также есть направления “вверх” и “вниз”, где “вниз” – это к центру шара, а “вверх” – от центра, как у нас на Земле. Топологическая размерность может быть даже 4 и больше, как мы видели во второй главе (например, тессеракт имеет топологическую размерность 4), но она всегда выражается целым числом. С фракталами, однако, дело обстоит по-другому. Фрактальная размерность показывает, грубо говоря, насколько хорошо кривая заполняет плоскость или насколько хорошо поверхность заполняет пространство.
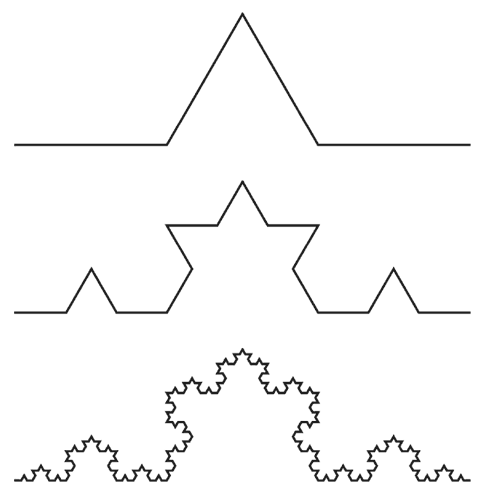
Первый, второй и четвертый этапы построения кривой Коха.

Снежинка Коха.





