Когда мы говорим, что нечто движется, мы подразумеваем, что оно меняет свое положение с течением времени. Это здравый смысл, но, чтобы быть точными, нам нужно удостовериться, что мы знаем, что мы имеем в виду под временем. И здесь перед нами встает та же дилемма реляционистского против абсолютистского.
Люди воспринимают время как изменение. Время наступления события измеряется относительно другого события — например, считывания показаний часов. Все показания часов и календарей суть относительные времена, точно как адреса суть относительные положения. Но Ньютон верил, что тут позади скрыто изменение абсолютного времени, которое воспринимает Бог.
Здесь есть привкус дебатов, которые бушевали с тех пор по проблеме абсолютного времени. Противник Ньютона Готфрид Лейбниц тоже верил в Бога, но его Бог был не свободен, тогда как Бог Ньютона делал так, как Ему нравится. Лейбниц поклонялся в высшей степени рациональному Богу. Но если Бог совершенно рационален, то все в природе должно иметь причину. Это и есть принцип достаточного обоснования Лейбница. Один из способов его формулировки такой, что каждый вопрос вроде «Почему вселенная такая, а не этакая?» должен иметь рациональный ответ. Конечно, имеются вопросы, на которые невозможно дать никакого рационального ответа. Точка зрения Лейбница заключалась в том, что задавать вопрос, который не может иметь рационально обоснованный ответ, означает совершать ошибку в мышлении.
Лейбниц пояснял свой принцип так: Он спрашивал, «Почему вселенная началась, когда началась, а не десятью минутами позже?» Он отвечал, что не может быть никакого рационального ответа, чтобы предпочесть историю вселенной другой истории, в которой все происходит на десять минут позже. Все относительные времена будут одинаковыми в обеих вселенных; только абсолютные времена будут различны. Но законы природы говорят только об относительных временах. Следовательно, утверждал Лейбниц, если нет причины для вселенной предпочесть начало в данное абсолютное время началу в другое, не может быть смысла в абсолютном времени.
Я поддерживаю рассуждения Лейбница, что когда бы я не ссылался на время, я буду подразумевать относительное время. В самом деле, хотя мы можем рассуждать о том, может ли быть некоторый трансцедентный смысл, в котором существует абсолютное время, несомненно то, что мы, люди, живущие в реальном мире, имеем доступ только к относительным временам. Так для целей описания движений мы будем рассматривать время, измеряемое часами. Для наших целей часами являются все приборы, которые считывают последовательность возрастающих чисел.
Теперь, когда мы определили как время, так и положение, мы можем переходить к измерению движения: Движение есть изменение положения, измеренного по отношению к некоторому эталонному объекту, в течение периода времени, измеренного по отношению к показаниям часов.
Это приводит нас к следующему ключевому шагу в нашем рассуждении. Чтобы делать науку, недостаточно просто давать определения и рассуждать о понятиях. Вы должны измерять движения. Это означает использовать инструменты вроде часов и линеек, чтобы соотнести положения и времена с числами.
В отличие от абсолютного положения, которое не наблюдаемо, относительные расстояния и относительные времена могут быть измерены в числах, которые, в свою очередь, могут быть записаны на куске бумаги или в цифровой памяти. Таким образом, наблюдения движения преобразуются в таблицы чисел, которые можно изучать методами математики. Один такой метод заключается в создании графика или диаграммы из записей, что переводит таблицу чисел в картинку, что может пробудить наше понимание и воображение.
Этот мощный инструментарий был разработан Рене Декартом, и преподается каждому школьнику. Несомненно, что-то похожее мог бы делать Кеплер, когда он боролся с данными Тихо Браге по орбите Марса. На Рис. 4 мы видим схему орбиты Луны по отношению к Земле.
В школе мы изучали второй способ рисовать движение, в котором добавляется ось для времени и рисуется положение в зависимости от времени. Это представляет орбиту как кривую в пространстве и времени, как на Рис. 5. Мы видим, что орбита Луны теперь представлена спиралью; пока она один раз возвращается к своему стартовому положению, проходит месяц.
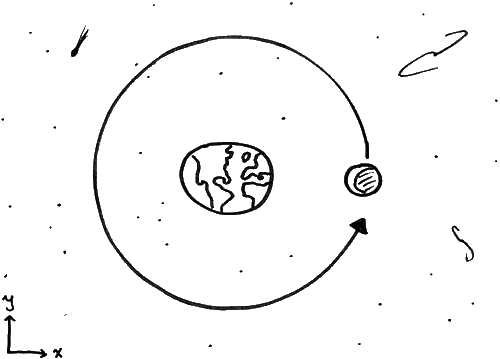
Рис. 4. Схема лунной орбиты вокруг Земли
Заметим, что путем графической записи наблюдений делается нечто удивительное. Кривая на Рис. 5 представляет измерения, выполненные, пока что-то эволюционирует во времени, но сами измерения от времени не зависят — что означает, однажды выполненные, они не меняются. И кривая, которая их представляет, также постоянна. Это означает, что мы сделали движение — то есть, изменение в мире — предметом изучения математики, которая изучает не меняющиеся объекты.
Способность заморозить время, как в приведенном примере, была для науки огромной поддержкой, поскольку мы не должны наблюдать движение, разворачивающееся в реальном времени; мы можем изучать записи прошлых движений, когда нам заблагорассудится. Но за пределами указанного удобства данное изобретение имеет чрезвычайные философские последствия, поскольку свидетельствует в пользу утверждения, что время есть иллюзия. Метод замораживания времени работал настолько хорошо, что большинство физиков не подозревают, что эта уловка действует на их понимание природы. Эта уловка была большим шагом в изгнании времени из описания природы, поскольку она побуждает нас заинтересоваться корреляцией между реальным и математическим, ограниченным во времени и вечным.
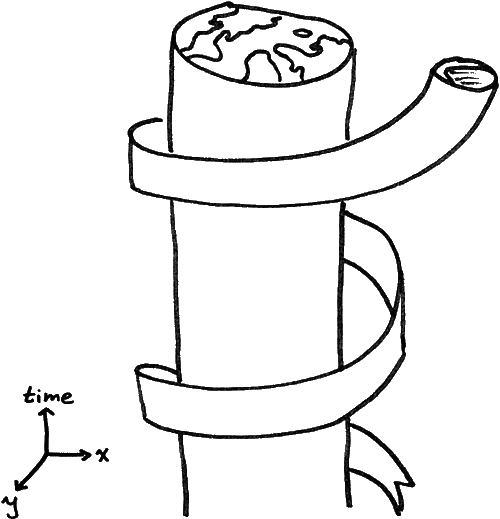
Рис. 5. Схема лунной орбиты как кривой в пространстве и времени
Эта корреляция настолько важна, что я хочу обрисовать ее на повседневном примере. Все эти непростые проблемы полностью проявляются в известной всем игре в мяч.
* * *
Около 1:15 пополудни 4 октября 2010 в восточной части Хай Парка в Торонто писатель-романист по имени Дэнни, бросает теннисный мяч, который он нашел этим утром в своем комоде для носков, поэтессе Джанет, с которой он только что познакомился.
Чтобы изучить бросок Дэнни с точки зрения физики, проделаем то же самое, что Браге и Кеплер сделали для Марса. Мы наблюдаем движение и записываем положения мяча в последовательные моменты времени; затем чертим результат в виде графика. Чтобы это выполнить, нам нужно задать положение мяча относительно некоторого объекта, в качестве которого мы можем выбрать самого Дэнни. Кроме этого, нам нужны часы.
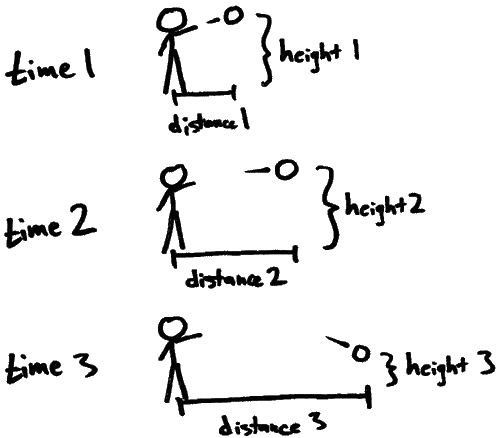
Рис. 6. Измерение броска Дэнни





