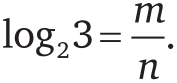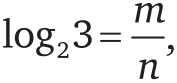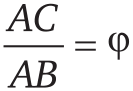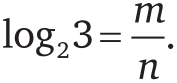
Исходя из определения логарифма и законов операций со степенями, из этого следует, что 2 m/n = 3, а (2 m/n)n = 3n, а следовательно, 2 m = 3n.
Однако никакая степень 2 не может быть равна какой бы то ни было степени 3
[28]: 2 в любой степени всегда дает четное число, а 3 в любой степени – нечетное. Значит, мы пришли к противоречию. Другими словами, не существует таких чисел m и n, для которых
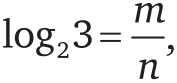
что означает, что m/n не может быть рациональным. Следовательно, log23 – иррациональное число.
Пять головоломок
1. Докажите, что золотое сечение
{22} ϕ
[29] – иррациональное число.
2. Символом секты пифагорейцев была пентаграмма, вписанная в пятиугольник.
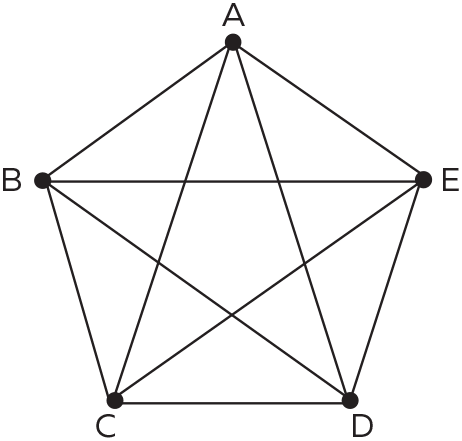
Докажите, что отношение длины диагонали правильного пятиугольника к длине одной из его сторон иррационально. Покажите также, что это отношение равно не произвольному иррациональному числу, а числу ϕ (см. предыдущую задачу). Другими словами, отношение любой диагонали этой фигуры к любой ее стороне равно золотому сечению!
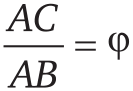
Как же повезло Пифагору, что он так и не узнал, что эти нахальные иррациональные числа, которые он не желал считать равноправными членами семейства чисел, скрывались даже в его собственной эмблеме!
Пифагорейский символ можно дополнить следующим образом:
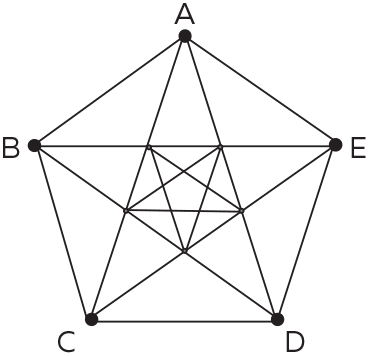
И такие «дополнения» можно продолжать до бесконечности!
1. Рационально ли число 0,07007000700007…?
2. Рационально ли число 0,123456789101112…?
3. А как насчет числа 0,01123581321345589144…, образованного из членов последовательности Фибоначчи – 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55… (эта последовательность начинается с 0 и 1, после чего каждый следующий член равен сумме двух предыдущих)?
5
Черепаха, Ахиллес и стрела: апории Зенона
Страх бесконечности, присущий древним грекам, замечательно выражается в знаменитых апориях
[30] Зенона Элейского, родившегося около 490 г. до н. э. Он в основном работал в Греции
[31] около 450 г. до н. э. О жизни Зенона известно мало. По-видимому, он провел большую ее часть на родине, в городе Элее, хотя Платон рассказывает нам в диалоге «Парменид» об интереснейшей встрече в Афинах, на которой присутствовали Зенон, Парменид и молодой Сократ.
Первоисточник Зенона не сохранился, и исследователи по большей части ссылаются на Аристотеля, который пересказывает апории Зенона в своей «Физике».
Зенон создавал свои апории на основе философии своего учителя и друга Парменида. Поэтому, прежде чем мы перейдем собственно к апориям Зенона, давайте узнаем кое-что о Пармениде и его необычной философии.
Взгляды Парменида на жизнь
Парменид, учитель и друг Зенона (Платон намекал даже, что Зенон с Парменидом были любовниками
[32]), считается явлением исключительным не только в греческой философии, но и во всей истории западной философии. Единственная известная работа Парменида «О природе», написанная в форме поэмы, дошла до нас лишь в отрывках. Парменид описывает два взгляда на реальность: «путь истины» и «путь чувств». Говоря о «пути истины», он объясняет, что реальность безвременна, однородна, бесконечно плотна и неизменна. Говоря о «пути чувств», он объясняет мир кажущегося и мнений, ложный и обманчивый. Жизненная философия Парменида состояла в том, что мир чувств – всего лишь иллюзия, а истинная Вселенная, которую можно познать только путем строгих размышлений, безмолвна и неподвижна. Он утверждал, что истинная Вселенная находится сейчас точно в том же состоянии, в котором она находилась секунду назад, год назад, миллиард лет назад, – и пребудет в нем же вовеки.
Что??? Это утверждение кажется несусветным даже для греческого философа.
Вот в чем заключалась суть его философии и каким образом он к ней пришел.
Парменид искал истины столь очевидной, что любые сомнения относительно ее справедливости были бы невозможны. Он хотел положить такую несомненную истину в основу всей своей философии. В математике такая истина называется аксиомой. Проведя много дней в утомительных размышлениях, Парменид заснул, и во сне ему явилась Афина – богиня мудрости, дочь Зевса и покровительница города Афин, – которая и помогла ему найти то, что он искал: То, что есть, есть, а того, чего нет, нет.
То есть Парменид утверждает, что существующее есть, а несуществующего нет. Это утверждение кажется очевидным и неопасным. Вы уверены? Тогда читайте дальше.