Вооружившись этой аксиомой, Парменид сформулировал несколько новых истин (на языке математики они называются теоремами). Сперва он предложил Первую теорему Парменида:
Существующее (то, что есть) не могло быть создано и не может исчезнуть.
Эта теорема доказывается почти мгновенно. В математике мы называем этот метод (как уже было упомянуто в другом месте) «доказательством от противного»: мы предполагаем, что справедливо обратное утверждение – что «то, что существует» когда-то было создано, – и проверяем, приводит ли это к логическому противоречию. Если приводит, это означает, что исходное предположение было неверным.
Если «то, что существует» было создано, оно должно было быть создано из чего-то, либо из того «что есть», либо из того «чего нет». Ничто не может быть создано из того «чего нет», потому что там ничего нет. Но, если «то, что существует» было создано из чего-то «что есть», это значит, что «то, что существует» уже существовало. Следовательно, «то, что существует» никогда не было создано.
Ч. т. д.
Предлагаю хитроумному читателю самостоятельно доказать аналогичным образом, что «то, что существует», никогда не может исчезнуть.
Затем философ доказал свою Вторую теорему Парменида:
Все существующее равномерно и бесконечно плотно.
Доказательство этого утверждения тоже поразительно просто. То, что существует, должно быть бесконечно плотным, потому что, если это не так, значит, оно содержит по меньшей мере некоторое количество «того, что не существует». Но «того, что не существует» не существует. Мнение Парменида, что «того, чего нет» нет, многократно истолковывалось в смысле отрицания пустоты. Пустота – это «то, чего нет», а следовательно, ее не существует.
Аналогичным образом все то, что существует, должно быть равномерное плотным, потому что, если есть нечто, что существует и обладает меньшей плотностью, это значит, что в нем больше «того, что не существует». Но «того, что не существует» не существует!
Опять же ч. т. д.
Вам уже кажется, что происходит нечто странное? То ли еще будет!
Великая теорема Парменида: Движение есть иллюзия
Доказательство этого утверждения совершенно очевидно: если все бесконечно плотно, как может быть возможно движение?
Тот факт, что мало кто отрицает существование движения, Парменида совершенно не заботил. Его не интересовал мир чувств и мнений, в котором существует возможность ошибки. В его мире истины (мире аксиом и теорем) все неподвижно, ничто не создается и ничто не исчезает.
Апория № 1. Дихотомия, или Иллюзия движения
Вернемся к Зенону. В той единственной книге, которую он, по-видимому, написал, он пытался защищать философию своего наставника. В частности, он хотел подкрепить утверждение Парменида относительно невозможности движения – утверждение, за которое Парменида больше всего критиковали, если не сказать высмеивали. И действительно, верить, что движения не существует, – занятие очень странное.
Защищая своего учителя, Зенон изложил свои знаменитые апории, которые увлекают бесчисленных математиков и философов вот уже более двух тысяч лет. В число тех, кто всерьез размышлял над ними, пытаясь понять, входят Аристотель, Маймонид, Декарт, Лейбниц, Спиноза, Бергсон, Рассел, Льюис Кэрролл, Кафка, Сартр, Гегель и Ленин (который прочитал об апориях в книге Гегеля и написал в своих «Философских тетрадях», что они совсем неплохи) – а также многие, многие другие.
Что же это за апории?
Первая апория называется «Дихотомия», и в ней Зенон демонстрирует невозможность движения при помощи чрезвычайно рационального и логичного объяснения.
Посмотрите на приведенный ниже чертеж. Зенон утверждает, что, чтобы попасть из точки А в точку В, необходимо пройти расположенную посередине между ними точку С.
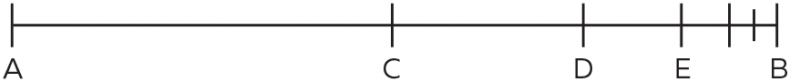
Но, чтобы попасть из С в В, необходимо сначала пройти половину расстояния между ними и добраться до точки D. Однако и попав в эту точку, особо радоваться не следует, так как, чтобы добраться из нее до точки В, теперь необходимо сначала преодолеть половину оставшегося расстояния и попасть в точку Е. И так далее и так далее.
Вот рассуждение Зенона: «Невозможно пройти бесконечное число точек за конечное время. Следовательно, попасть из точки А в точку В вообще невозможно». Наконец-то мы понимаем, как решить задачу, в которой спрашивается «сколько времени понадобится поезду, чтобы прибыть в одну точку, после того, как он выйдет из другой точки?». Правильный ответ – этот поезд никогда никуда не придет. А поскольку точки А и В выбраны совершенно произвольно, отсюда следует, что переместиться из любого места в любое другое также невозможно. Следовательно, невозможно и движение.
Во множестве книг излагается разрешение этого противоречия. Рассуждение движется (Зенон резко возражал бы против использования слова «движется») более или менее по следующему пути: предположим, что время, необходимое для преодоления определенного расстояния, пропорционально его величине. Тогда мы можем доказать, что Зенон был неправ, потому что все бесконечные «половинные расстояния» (которые становятся все меньше и меньше) можно преодолеть за конечное время. Например, если предположить, что перемещение из точки А в точку С занимает в точности одну единицу времени – скажем, минуту, – то перемещение из точки С в точку D займет полминуты (поскольку это расстояние равно половине предыдущего), из точки D в точку Е – четверть минуты и так далее. Обозначим суммарное время, требуемое для перемещения из А в В, буквой S:
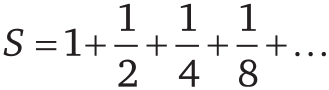
Разделив обе части на 2, получим:
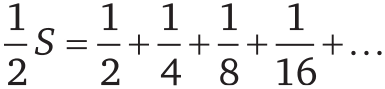
Вычтем второе равенство из первого:
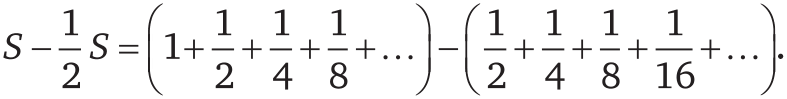
.
Следовательно,
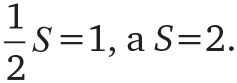
Другими словами, преодоление бесконечного числа серединных точек между А и В займет ровно две минуты.

