Теперь мы можем выписать все уравнения (некоторые из которых не имеют решений) в порядке возрастания высоты.
Например, для Н = 1 существует всего один многочлен, и он представляет собой просто 1, то есть не зависит от х, и дает уравнение 1 = 0, не имеющее решений. Это уравнение не имеет смысла и не дает нам никаких алгебраических чисел.
Для Н = 2 мы получаем два уравнения: х = 0 и 2 = 0. Первое дает алгебраическое число 0, а второе снова оказывается бессмысленным и не имеет корней.
Для Н = 3 получаются следующие уравнения: 3 = 0, х – 1 = 0, 2х = 0, х + 1 = 0, и наконец, х² = 0. Первое из этих уравнений не дает алгебраических чисел, а из остальных мы получаем два новых алгебраических числа: 1 и –1.
Я надеюсь, что основная идея понятна.
Дойдя до Н = 5, мы встретимся с √2 (убедитесь в этом самостоятельно). Для каждого значения высоты существует конечное количество уравнений, и каждое уравнение имеет конечное число решений; следовательно, при каждом значении высоты мы добавляем конечное количество алгебраических чисел. Это доказывает, что множество алгебраических чисел – это на самом деле набор, состоящий из счетного числа конечных множеств. Следовательно, алгебраические числа легко можно разместить в бесконечной гостинице Гильберта. Это означает также, что множество алгебраических чисел счетно и его мощность – ℵ0.
В это довольно трудно поверить, но мощность множества чисел, делящихся на пухплекс в степени пухплекса, равна мощности множества алгебраических чисел.
ℵ: бо́льшая бесконечность – мощность континуума
Доказать, что множество счетно, совсем не трудно. Нужно всего лишь найти одно-однозначное и сюръективное соответствие с множеством натуральных чисел. Проблема сводится к следующему: чтобы доказать, что то или иное множество счетно, достаточно показать, что его элементы могут быть расположены в некотором последовательном порядке, но, чтобы доказать, что множество несчетно, необходимо доказать, что не существует абсолютно никакого способа расположить его элементы последовательно. Это похоже на «задачу» доказательства, что в комнате есть по меньшей мере один муравей, в сравнении с задачей доказательства, что нигде в комнате ни одного муравья точно нет. Как только мы найдем хотя бы одного муравья, мы получим доказательство первого утверждения, но то, что мы не находим муравьев в данный момент, совершенно не означает, что какой-нибудь муравей не найдется позже.
Как я уже отмечал, в 1891 г. Георг Кантор предложил замысловатый метод, помогающий доказать невозможность подсчета количества разнообразных объектов, – он называется «диагональным методом Кантора». Мы уже встречались с этим методом, когда профессор Финкельштейн-Островский-Канторович доказывал, что в бесконечной гостинице невозможно разместить числа, заключенные между 0 и 1, десятичное представление которых содержит только цифры 0 и 1. При помощи того же самого метода можно доказать, что и множество всех чисел, заключенных между 0 и 1, несчетно (докажите это!). В этом нет ничего неожиданного, поскольку множество «чисел, заключенных между 0 и 1, десятичное представление которых содержит только цифры 0 и 1» – это собственное подмножество множества всех чисел, заключенных между 0 и 1. Кроме того, если вспомнить, что любое существующее число может быть записано в двоичной системе счисления с использованием только цифр 0 и 1, можно легко убедиться, что мощность этих двух множеств должна быть одинаковой (почему?).
Бесконечные множества чисел, которые невозможно расположить в последовательном порядке, называются – что и неудивительно – несчетными. Множество всех точек на числовой прямой, заключенных между 0 и 1, несчетно, и его мощность не равна ℵ0. Следовательно, для обозначения мощности множества всех вещественных чисел (или любого отрезка прямой вещественных чисел) нужен новый символ! В качестве такого символа используют букву ℵ
[50]. Говорят, что ℵ – мощность континуума. Однако следует отметить, что несчетные множества не всегда имеют мощность ℵ.
Слова, слова, слова
Поскольку концепция канторовой диагонали не только красива, но и важна, я объясню ее еще раз – теперь на примере доказательства, что множество всех слов бесконечной длины, составленных с использованием только двух букв (a и b), невозможно подсчитать. Другими словами, такое множество несчетно.
Если вы уже поняли объяснение, которое профессор Финкельштейн-Островский-Канторович дал Омеге относительно чисел в десятичной системе счисления, у вас не должно вызвать затруднений и следующее изложение. Речь идет в точности о том же самом, только на другом примере. Если вы не вполне поняли первое объяснение, я надеюсь, что вы поймете его на этот раз.
Доказательство будет строиться от противного, то есть мы предположим, что справедлива противоположная гипотеза: все такие слова можно расположить в некой последовательности. Затем мы увидим, что это предположение приводит к противоречию, что означает, что наша исходная гипотеза была ложной.
Вот расположение слов:
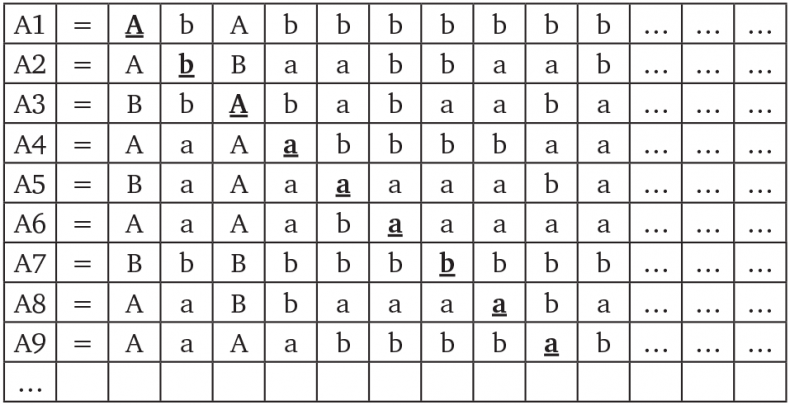
Применяя диагональный метод Кантора, аналогично тому, как мы действовали с числами, заключенными между 0 и 1, образуем новое слово А0, которое не содержится где бы то ни было в представленном в таблице множестве, в каком бы порядке мы ни располагали слова. Внимательно посмотрите на таблицу и обратите внимание на подчеркнутые буквы, стоящие на диагонали. Новое слово А0 будет построено следующим образом: его первая буква будет отличной от первой буквы слова А1 (поскольку первая буква в А1 – а, мы возьмем букву b); вторая буква будет отличной от второй буквы слова А2 (раз это буква b, мы используем букву а); третья буква будет отличной от третьей буквы слова А3 (на этот раз возьмем букву b) – и так далее.
Итак, наше новое слово A0 = babbbbabb…
Я предоставлю умудренному читателю самостоятельно убедиться, что слово А0 никоим образом не может встретиться в исходном бесконечном списке (то есть совпасть с каким бы то ни было его словом), потому что оно не может не отличаться от любого слова Ai по меньшей мере буквой, стоящей на i-м месте.
К тому же, как уже выяснила Омега, добавление слова А0 в список ничего не меняет, потому что мы всегда можем повторить ту же процедуру и построить еще одно слово, назовем его Aℵ, которое будет отличаться от всех без исключения слов, включенных в составленный нами бесконечный список. Итак, множество всех слов бесконечной длины, содержащих только буквы a и b, имеет мощность континуума.
Очевидно, множество всех слов бесконечной длины, составленных с использованием трех разных букв (а не только букв a и b) или четырех или пяти (или любого другого количества) разных букв, также должно иметь мощность несчетного множества, что само по себе не означает, что его мощность будет равна мощности континуума. Однако, поскольку мы можем построить между таким множеством и множеством чисел, составленных из 0 и 1, одно-однозначное и сюръективное отображение, мы видим, что его мощность действительно равна ℵ.



