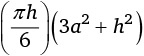
Валькнут
43. КАРТИНА НА СТЕНЕ

Обычно, чтобы повесить картину на двух гвоздях, веревку цепляют за оба гвоздя, как показано на рисунке.
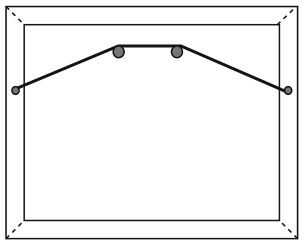
Преимущество такого способа состоит в том, что, если один гвоздь выпадет, картина продолжит висеть, поскольку будет держаться на втором гвозде.
Сможете ли вы придумать способ так обернуть веревку вокруг гвоздей, чтобы картина падала на пол при извлечении одного из них? (В случае необходимости веревку можно удлинить.)

Кольца и предметы домашнего обихода естественным образом приводят нас к математической идее кольца для салфеток. Именно такая фигура получится, если просверлить цилиндрическое отверстие в шаре таким образом, чтобы центр отверстия проходил через центр шара.
Следующая головоломка особенно интересна тем, что в ней очень мало данных.
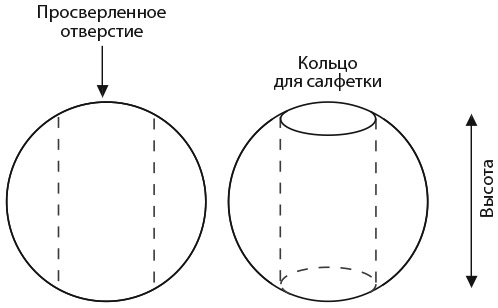
44. ПРИМЕЧАТЕЛЬНОЕ КОЛЬЦО ДЛЯ САЛФЕТОК

Высота кольца для салфеток – 6 сантиметров. Чему равен его объем?
Решение этой головоломки предполагает большое количество рутинной работы, но пусть вас это не пугает. Я помогу вам начать ее решать. Поверьте, это потрясающая задача.
Объем кольца для салфеток равен разности между объемом шара и объемом подлежащей удалению центральной части в виде цилиндра с выпуклыми верхней и нижней поверхностями – куполами.
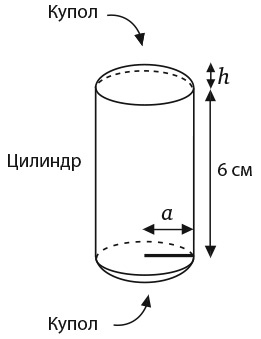
Высота цилиндра составляет 6 сантиметров. Пусть r – радиус шара, h – высота купола, a – радиус поперечного сечения цилиндра, который также является радиусом основания купола. Далее вам понадобятся только формулы объема, которые я с удовольствием привожу ниже.
Формула объема шара:
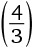 πr3
πr3
Формула объема цилиндра: πa2 × 6 см, или 6πa2
Формула объема каждого купола:
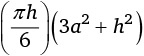
Мы уже близки к решению. Объем кольца для салфеток равен объему шара минус объем цилиндра минус двойной объем купола. С помощью теоремы Пифагора мы можем выразить a через r, а также h через r. Следовательно, можно записать объем кольца для салфеток в виде выражения, в котором r – единственная переменная. Это будет длинное выражение, содержащее множество r и π.
Чего же вы ждете?!
Историк Геродот писал, что геометрия была изобретена в Египте при измерении площади участков пахотной земли, затопленной Нилом. Вычисление площади квадратов и прямоугольников до сих пор остается одной из первых задач, которые мы изучаем в геометрии. Для этого необходимо умножить одну сторону на другую, смежную.
Эта простая процедура – все, что вам нужно для решения головоломки под названием Menseki Meiro («Неразбериха с площадями»), придуманной японским изобретателем Наоки Инаба.
Далее вы увидите пример такой головоломки и сможете разобраться в ее сути. Ваша задача – найти отсутствующее значение. Обозначенные на рисунке расстояния не соответствуют реальным размерам фигур, поэтому получить ответ посредством измерения не получится.
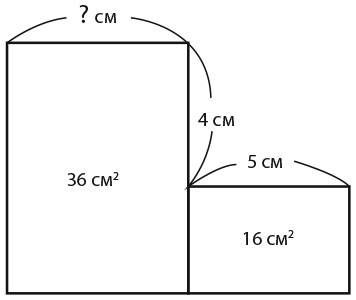
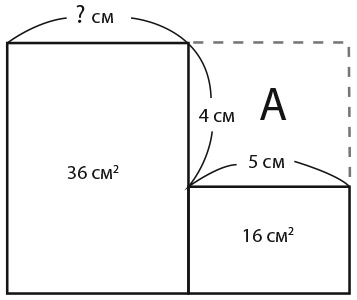
Красота этой головоломки в том, что решить ее вы должны геометрически, с помощью целых чисел. Не разрешается портить свою работу уравнениями или – боже упаси! – дробями. Для того чтобы справиться с задачей, дополните большой прямоугольник так, как показано на рисунке ниже. Площадь прямоугольника A должна составлять 20 см2, так как равна 4 × 5 сантиметров. Это означает, что сумма площадей прямоугольника A и нижнего прямоугольника равна 20 + 16 = 36 см2, что эквивалентно площади большого прямоугольника слева. Поскольку прямоугольники имеют одинаковую высоту, у них должна быть и одинаковая ширина, а значит, отсутствующее значение – 5 сантиметров.
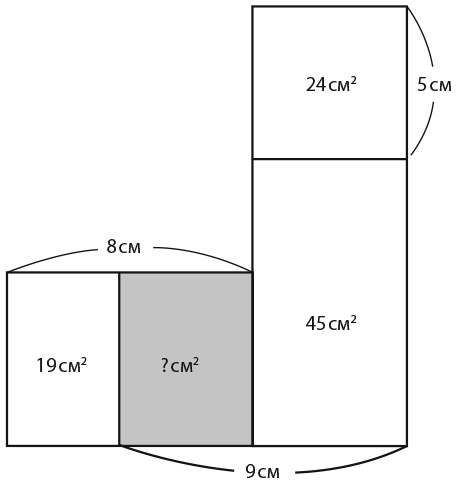
45. НЕРАЗБЕРИХА С ПЛОЩАДЯМИ
Найдите отсутствующее значение.
Наоки Инаба, пожалуй, самый плодовитый и блестящий разработчик дедуктивных головоломок из всех современных специалистов в этой области, хотя о его работе мало кто знает за пределами родины. Благодаря таким людям, как Инаба, а также компании Nikol в Японии сформировалось, возможно, самое активное сообщество любителей головоломок в мире.









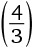 πr3
πr3