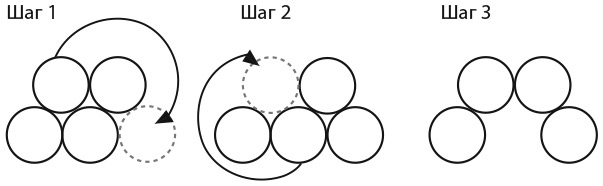
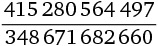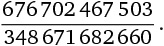Решение сводится к следующему. Сначала необходимо понять, как зафиксировать относительное положение четырех монет. Существует только один способ это сделать – расположить четыре монеты в форме ромба, как показано на рисунке ниже (шаг 1). Для того чтобы закрепить относительное положение монет, нужно передвинуть любую монету в новое положение так, чтобы она соприкасалась с двумя другими.
Таким образом, нам придется перейти от схемы расположения монет, показанной в шаге 1, к представленной выше начальной схеме, придерживаясь следующего правила: на каждом шаге монету нужно размещать так, чтобы она соприкасалась с двумя другими – см. рисунок (шаг 2 и шаг 3).
Головоломки с монетами – это увлекательные маленькие задачки, которые полностью захватывают ваше внимание до тех пор, пока вы не найдете их решение. Как правило, они гораздо сложнее, чем кажется на первый взгляд. Тем не менее, немного подумав, вы сможете их решить.
Описанную выше задачу сто лет назад придумал английский математик Генри Дьюдени. Авторство следующей задачи тоже принадлежит ему.
76. 6 МОНЕТ
Расположите шесть одинаковых монет на столе по схеме, изображенной на рисунке, так, чтобы седьмую монету можно было разместить в заштрихованной области, соприкасающейся со всеми монетами.
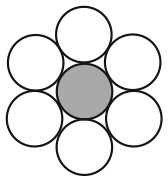
Сначала необходимо определить начальное положение для всех шести монет. Затем поочередно передвигать монету на новое место так, чтобы она при этом соприкасалась с двумя другими монетами.
Задача решается за три шага.
Головоломки с монетами весьма увлекательны. Стоит вам разгадать эту, как захочется решить еще одну, и еще…
77. ПРЕВРАЩЕНИЕ ТРЕУГОЛЬНИКА В ЛИНИЮ
Можете ли вы превратить треугольник в линию за семь шагов? Как и ранее, с каждым шагом нужно передвигать монету в новое положение так, чтобы она соприкасалась с двумя другими монетами. Запрещается отрывать монету от стола или с ее помощью передвигать другую монету.
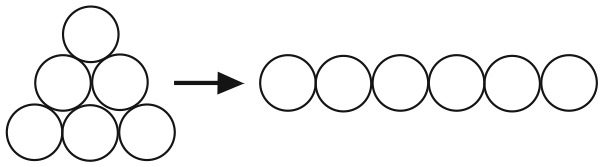
Для решения следующей задачи понадобится восемь одинаковых монет.
78. ВОДНАЯ ГОЛОВОЛОМКА
[25]
Придерживаясь тех же правил перемещения монет, что и в предыдущих задачах, сможете ли вы превратить букву H в O за четыре шага?
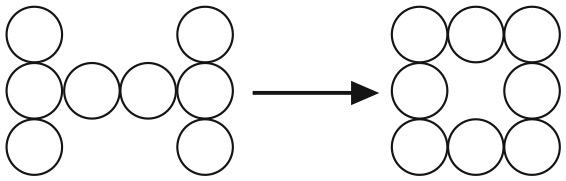
А можете ли вы вернуться от O к H за шесть шагов?
Мы уже встречались с Генри Дьюдени в этой книге. Он автор головоломки о Смите, Джонсе и Робинсоне, публикация которой вызвала всплеск интереса к решению дедуктивных задач в 1930-х годах.
Дьюдени был величайшим новатором по части придумывания головоломок в Великобритании, а возможно, и во всем мире. За сорок лет работы в газетах и журналах он составил больше классических задач по занимательной математике, чем кто-либо. В этом смысле Дьюдени был очень плодовит. Как говорилось в главе 1, задача о Смите, Джонсе и Робинсоне (задача 7) была опубликована в колонке Perplexities, которую Дьюдени много лет вел в журнале Strand, в 1930 году, в том самом месяце, когда он ушел из жизни.
По всей вероятности, призванием Дьюдени обязан своему деду, пастуху из Южного Даунса, который самостоятельно освоил математику и астрономию. Впоследствии он стал школьным учителем, как затем и его сын. Генри Дьюдени родился в 1857 году, но он не был создан для работы в сфере формального образования. Вместо того чтобы учиться в школе, в возрасте 13 лет он поступил работать клерком в государственное учреждение в Лондоне. Со временем жизнь служащего наскучила Дьюдени, и он начал отправлять придуманные им головоломки в редакции национальных изданий. Вскоре Дьюдени бросил работу, чтобы полностью посвятить себя созданию головоломок.
Его работа отличается не только размахом, но и глубиной, что особенно удивительно для самоучки, а живой арифметический ум не имел равных. В одной задаче из его книги The Canterbury Puzzles
[26] 1907 года сказано, что куб единицы и куб двойки дают в сумме девять (13 + 23 = 1 + 8 = 9). Далее автор предлагает читателю найти еще два числа, сумма кубов которых равнялась бы девяти. Вот ответ:
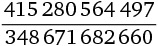
и
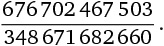
«Один известный клерк страховой компании и один корреспондент взяли на себя труд возвести в куб эти числа, и оба нашли мой ответ совершенно правильным», – писал Дьюдени. Разум приходит в ужас при мысли о том, что он сумел получить этот результат исключительно с помощью бумаги и карандаша.
Дьюдени – автор многих головоломок с монетами. Следующая взята из его книги Amusements in Mathematics («Математические развлечения»), опубликованной в 1917 году.
79. 5 ПЕННИ
Это очень сложная задача, хотя ее условия до смешного просты. Каждый читатель знает, как разместить четыре монеты по 1 пенни так, чтобы они были равноудалены друг от друга. Для этого нужно всего лишь положить их горизонтально на стол таким образом, чтобы они, соприкасаясь друг с другом, образовали треугольник, а четвертую монету поместить сверху, в центре. В этом случае каждое пенни соприкасается со всеми остальными, поэтому все монеты находятся на равном расстоянии друг от друга. Теперь попытайтесь сделать то же самое с пятью пенни. Разместите их так, чтобы каждая монета соприкасалась со всеми остальными, – вы обнаружите, что это совсем другое дело.