Витгенштейн отвергает подобную позицию в отношении кванторов. Метод логического анализа Рассела является неприемлемым, поскольку вынуждает принять, так сказать, «божественную» точку зрения на мир в целом. В свете «Трактата» это было бы равносильно попытке сказать то, что может лишь показать себя: я не могу сказать, что то или это является «объектом», это может лишь показать себя в том факте, что я использую имя собственное; аналогичным образом я не могу сказать, что не существует других людей, помимо перечисленных мною в вышеупомянутом списке, это может лишь показать себя в том факте, что в моем языке не находится других имен людей.
Итак, последние замечания приводят Витгенштейна к признанию следующего: сложное предложение, независимо от того, имеется ли в нем квантор всеобщности («для всех х») или квантор существования («существует по крайней мере один х, такой, что»), является не более чем составным высказыванием для выражения конъюнкции или дизъюнкции предложений, полученных посредством замены квантифицированной переменной именами собственными. Дополнительное условие – «не существует других людей, помимо», – наличие которого Рассел считал необходимым, попросту исчезло.
Таким образом, данное положение позволяет свести сложные предложения к молекулярным, к конъюнкции или дизъюнкции элементарных предложений. Другими словами, появилась возможность устранить то, что казалось как Фреге, так и Расселу логическими постоянными, а именно: «для всех х» и «существует по крайней мере один х, такой, что».
Что же тогда можно сказать в отношении молекулярных предложений или, если угодно, других логических постоянных, которыми являются пропозициональные связки? Можно ли их тоже устранить, или мы должны признать, что они добавляют что-то к значению предложений, в которых содержатся?
Для ответа на этот вопрос нам потребуется вспомнить, каким образом Фреге и Рассел использовали логические связки, о чем уже вкратце упоминалось. Рассмотрим, к примеру, следующее молекулярное предложение: «Ширак болен, и телевизор выключен». Что может означать «и»? Самый простой ответ: «и» указывает на то, что предложение является истинным, если хотя бы одно из элементарных предложений, входящих в его состав (или оба), является истинным. Мы можем подобным образом подойти к другим логическим связкам вроде «или», «если… то» и т. д. Впрочем, в этом нет ничего нового: схожее определение связок, как отмечалось выше, мы обнаруживаем не только у Фреге с Расселом, но и у стоиков в Античности.
Приняв вышесказанное за основу, Витгенштейн переходит к общим выводам. В молекулярном предложении определенным образом сочетаются элементарные предложения, которые входят в эти сочетания как обладающие общей формой, то есть как способные быть истинными или ложными (как говорящие, что дело обстоит так-то и так-то).
В целях упрощения рассмотрим только два возможных положения вещей, α и β, отображенные соответственно двумя элементарными предложениями – p и q. Напомним, что простые положения вещей являются взаимно независимыми, то есть существование или несуществование одного простого положения вещей совершенно не зависит от существования или несуществования другого простого положения вещей. Поэтому α и β могут сочетаться ни много ни мало четырьмя разными способами. Если мы условимся обозначать α тот факт, что α не существует, у нас получится четыре возможных сочетания: {<α, β>, <α, β>, <α, β>, <α, β>} (при наличии 3 положений вещей получилось бы соответственно 8 возможных сочетаний, и т. д.).
Итак, можно сказать, что форма возможной сложной ситуации, состоящая из двух положений вещей α и β, является совокупностью четырех возможных сочетаний, так же как и форма возможного положения вещей является совокупностью способов, которыми сочетаются простые объекты, составляющие его. Легко установить, что оба элементарных предложения p и q, если принимать во внимание исключительно их истинность или ложность, также могут сочетаться лишь четырьмя разными способами; если мы условимся обозначать pv тот факт, что p является истинным, а pf – тот факт, что p является ложным, у нас получится: {<pv, qv>, v, qf>, <pf, qv>, f, qf>}; таким образом эти четыре возможности элементарных предложений быть истинными или ложными соответствуют четырем возможностям положений вещей α и β быть существующими или несуществующими.
О чем говорит элементарное предложение? О том, что положение вещей, которое оно отображает, является существующим. О чем говорит молекулярное предложение, состоящее из p и q? О том, что некоторые, все или ни одно из четырех сочетаний {<α, β>, <α, β>, <α, β>, <α, β>} не являются существующими. Например, p или q говорит, что α и β являются существующими, или что α является существующим, или что β является существующим, и исключает то, что ни α, ни β не являются существующими. Другими словами, с одной стороны, это предложение выражает согласие с тремя первыми возможностями <α, β>, <α, β>, <α, β>, с другой – несогласие с возможностью <α, β>. Следовательно, в отличие от элементарного предложения, которое является истинным только при условии, что отображаемое им положение вещей является существующим, молекулярное предложение типа p или q является истинным только при условии, что одно из трех возможных сочетаний <α, β>, <α, β> или <α, β> является существующим. Таким образом, «условия истинности» p или q состоят в том, что p и q являются одновременно истинными, или в том, что p является истинным, или, наконец, что q является истинным.
До этого мы признавали, что знаем значение связки «и», для понимания которого одной записи p или q недостаточно. Тем не менее легко определить это значение с помощью следующей символики:
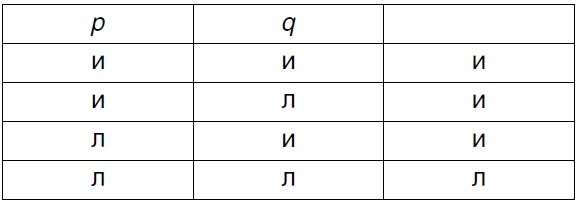
Буква «и» означает «истинное», буква «л» – «ложное», а правый столбец указывает, с какими «истинностными возможностями» p и q согласуется молекулярное предложение. Истинностные возможности, с которыми предложение согласуется, Витгенштейн называет основаниями истинности этого предложения. Таким образом, в правом столбце указано, каковы основания истинности молекулярного предложения. Здесь мы имеем дело с пропозициональным знаком, в котором слово «и» больше не присутствует и достоинством которого является то, что он прямо показывает, каковы условия истинности молекулярного предложения. Запомнив порядок расположения истинностных возможностей p и q, мы сможем записать это предложение еще более кратко, в доступном для понимания виде: (v, v, v, f) (p, q).



