Когда я слышу слово «распределение» – представляю себе гистограмму частот появления значений. В нашем примере это будет гистограмма с диаметрами шаров. Мы работаем с непрерывными числовыми значениями, вся шкала гистограммы разбивается на диапазоны, как правило, равной длины (0–10, 10.01–20…). На основе гистограммы сложно принимать решения, поэтому в гипотезах обычно оценивают какой-то отдельный параметр распределения, например среднее или медиану. Строим по ним гистограмму (рис. 10.1).
Такие гистограммы (распределения) очень сложно сравнить друг с другом, поэтому и используются числовые статистики распределений.
Генеральная совокупность имеет свое распределение шаров, выборка – свое. Чем больше выборочное распределение похоже на распределение генеральной совокупности – тем лучше. Случайность вытаскивания шаров очень важна для этого – ведь шары в резервуар могли насыпать сначала одного диаметра, потом другого. Тогда на поверхности могут оказаться самые большие шары, и если мы их будем брать преимущественно оттуда, то наше распределение шаров внутри выборки окажется смещенным в сторону большего диаметра, поэтому наши выводы могут оказаться неверными.
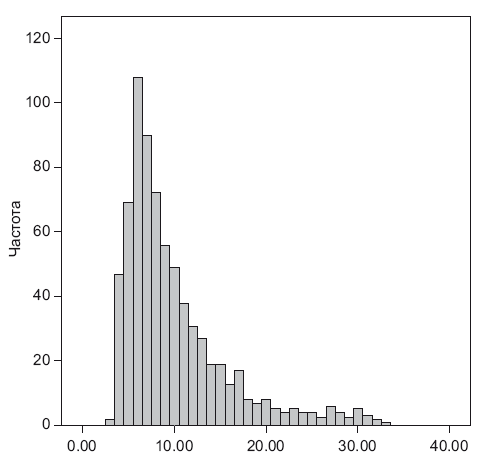
Рис. 10.1. Пример распределения
Возвращать шары нужно, чтобы работать с исходным распределением генеральной совокупности, так как каждое вытягивание будет независимо от предыдущих. Теперь давайте применим интуицию – чем больше шаров мы вытянем, тем лучше распределение выборки будет похоже на распределение в резервуаре, и тем выше точность оценки параметра в выборке мы получим. А сколько нужно вытянуть шаров, чтобы получить приемлемую точность? На этот вопрос уже ответит статистика – об этом чуть позже, а сейчас усложним задачу.
Теперь у нас есть два резервуара, нужно сравнить средний диаметр шаров между ними. Самое время перейти к формулировке гипотезы. Для этого нам понадобится сформулировать основную (H0) и альтернативную гипотезу (H1) с точки зрения статистики и проведения экспериментов:
• Нулевая гипотеза H0 (null hypothesis) утверждает, что метрика в эксперименте не изменилась и все наблюдаемые изменения случайны.
• Альтернативная гипотеза H1 (alternative hypothesis) утверждает, что метрика в эксперименте изменилась, наблюдаемые изменения не случайны.
Тестирование гипотез похоже на суд. Мы считаем, что обвиняемый невиновен, пока не будет найдено строгое доказательство, что он виновен. Аналогично с гипотезами [77], изначально считаем гипотезу H0 верной, пока не найдем доказательства, чтобы отклонить ее в пользу H1.
Теперь переформулируем эти общие утверждения для нашей задачи с двумя резервуарами в виде двусторонней гипотезы:
Гипотеза H0 утверждает, что средние диаметры шаров в обоих резервуарах равны μ1 = μ2.
Гипотеза H1 утверждает, что диаметры в обоих резервуарах разные —.
Можно также сформулировать в виде односторонней гипотезы:
Гипотеза H0 утверждает, что средний диаметр в первом резервуаре меньше или равен среднему диаметру во втором резервуаре —.
Гипотеза H1 утверждает, что средний диаметр в первом резервуаре больше среднего диаметра во втором резервуаре —.
С моей точки зрения, лучше использовать односторонние гипотезы. Ведь проверяя какую-либо идею, мы стремимся улучшить метрику, а значит, нас интересует вопрос, стало ли лучше (гипотеза H1). Дальше посмотрим, как статистика делает сравнение.
Статистическая значимость гипотез
Суд может ошибаться, тестирование статистических гипотез – тоже. Определим эти ошибки с помощью таблицы. Они бывают двух типов (табл. 10.1): ошибка первого рода, когда мы ошибочно отклонили нулевую гипотезу H0 (признали невиновного виновным), и ошибка второго рода, когда мы ошибочно приняли ее (признали виновного невиновным).
Таблица 10.1. Ошибки статистических гипотез

На языке статистики ошибки описываются вероятностями:
Вероятность ошибки 1-го рода:. Обычно исследователи используют = 0.05 (5 %).
Вероятность ошибки 2-го рода:. Величина (1 —) называется мощностью, которая является вероятностью найти улучшение, если оно есть.
Для упрощения тестирования гипотез Фишер [76] ввел величину p-значение (p-value), которая является мерой доказательства против нулевой гипотезы H0. Чем она меньше, тем сильнее доказательства против нулевой гипотезы. Важно заметить, что p-значение – это не вероятность правильности гипотезы H0, оно работает только для ее отвержения.
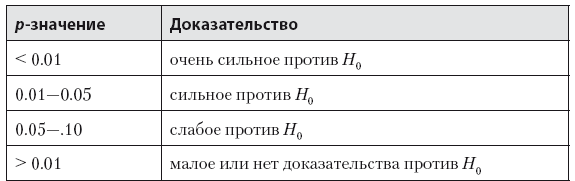
В традиционной, или, как я ее называю, фишеровской статистике, p-значение – это универсальное число, которое понятно статистикам и позволяет отвергать нулевую гипотезу. До Фишера использовались конкретные статистики, а не p-значение. Согласно книге Ларри Вассермана «All of Statistics: A Concise Course in Statistical Inference» [77], исследователи обычно используют следующую трактовку p-значения (табл. 10.2) (для = 0.05).
Таблица 10.2. Трактовка p-значений
Теперь посмотрим на графическую интерпретацию двусторонней гипотезы. На рис. 10.2 изображено сравнение распределения нулевой и альтернативной гипотез для нашего примера с двумя резервуарами.
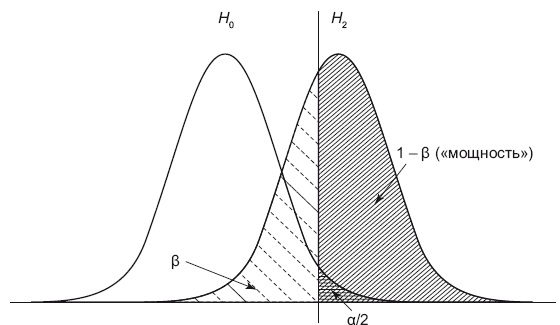
Рис. 10.2. Статистическая мощность
Каждое распределение представляет плотность вероятности. По сути это две гистограммы с площадью под каждой кривой, равной единице. На графике нулевой гипотезы мы отмечаем две вертикальные линии таким образом, что площадь каждой на хвосте была равна /2. В случае односторонней гипотезы строится только одна линия с площадью. Эта линия делит распределение альтернативной гипотезы на две части – и (1 —), площади под ними как раз и равны соответственно ошибке второго рода и мощности критерия. Из графика наглядно видно, что чем дальше находятся пики (средние) этих распределений, тем выше мощность и ниже ошибка второго рода (неверное принятие нулевой гипотезы). И это очень логично – чем дальше средние распределений находятся друг от друга, тем становится явнее разница между гипотезами, а значит, нам легче отвергнуть H0. С другой стороны, если «уже» распределения, то мощность растет, и нам также легче отвергнуть нулевую гипотезу. Увеличение числа данных в выборке (sample size) способствует «сжиманию» таких распределений.

