Именно таким образом работают калькуляторы мощности, которые вычисляют необходимый объем данных для тестов. В калькулятор вводится минимальная детектируемая разность в значениях параметров, уровень и ошибок. На выходе будет объем необходимых данных, которые нужно собрать. Закономерность здесь проста – чем меньшую разницу вы хотите детектировать, тем больше данных для этого нужно.
Альтернативой p-значению является доверительный интервал. Это интервал, внутри которого находится наш измеряемый параметр с определенной степенью точности. Обычно используют 95 %-ную вероятность (= 0.05). Если у нас есть два таких доверительных интервала для тестовой и контрольной группы, то по их пересечению можно понять, есть ли между ними отличие. P-значение и доверительные интервалы – это две стороны одной и той же медали. Интервал удобен для представления данных на графиках. Он часто используется в альтернативных методах оценок А/Б-тестов: байесовской статистике и бутстрэпе.
Статистические критерии для p-значений
Как мы уже узнали, p-значение – универсальная метрика тестирования гипотез. Для ее расчета нужно следующее: нулевая гипотеза, статистический критерий, односторонний или двусторонний тест, данные.
Чтобы определить p-значение, вам необходимо знать распределение выбранной статистики (статистического критерия), считая, что нулевая гипотеза верна. Далее с помощью кумулятивной функции распределения cdf (Cumulative Distribution Function) этой статистики мы можем вычислить p-значение, как проиллюстрировано на рисунке (рис. 10.3):
• Левостронний тест: p-значение = cdf(x).
• Правосторонний тест: p-значение = 1 – cdf(x).
• Двусторонний тест: p-значение = 2 × min(cdf(x), 1 – cdf(x)).
Сейчас проще не изобретать велосипед, а пользоваться готовыми калькуляторами в статистических пакетах или программных библиотеках. Важно только выбрать правильный статистический критерий.
Выбор такого критерия зависит от задачи:
• Z-тест для проверки среднего в нормально распределенной величине.
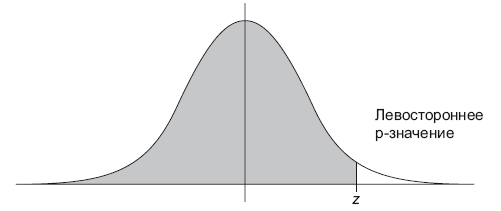
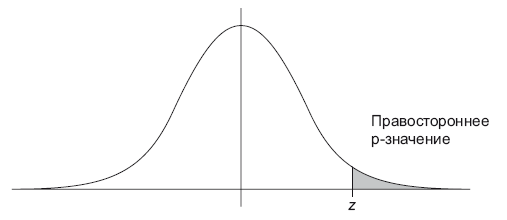
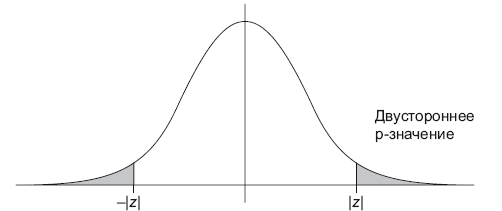
Рис. 10.3. Левосторонний, правосторонний, двусторонний тесты
• T-тест Стьюдента – то же самое, что и z-тест, но для выборок малого объема (t < 100).
• Хи-квадрат Пирсона для категориальных переменных и всяческих биномиальных тестов. Очень удобен для расчета конверсий, например посетителей в покупателей, где нужен биномиальный тест – купил или нет.
• Тест Стьюдента для двух независимо распределенных выборок очень хорошо подходит для нашей задачи с двумя резервуарами или для сравнения средней суммы покупки.
У таких тестов есть одна проблема – они привязаны к распределению. Например, для тестов Стьюдента и z-теста нужны нормально распределенные данные. Форма таких данных формирует «колокол» на гистограмме. Например, распределение средних чеков покупок не образует такого распределения. Конечно, можно их преобразовать логарифмированием и собрать в форму колокола, но часто это неудобно. Первой альтернативой для ненормально распределенных данных являются непараметрические тесты.
Хотя согласно статистическому словарю STATISTICA [78] – непараметрические методы наиболее приемлемы, когда объем выборок мал. Если данных много (например, > 100), то не имеет смысла использовать непараметрические статистики. Дело в том, что когда выборки становятся очень большими, то выборочные средние подчиняются нормальному закону, даже если исходная переменная не является нормальной или измерена с погрешностью. Непараметрические тесты имеют меньшую статистическую мощность (менее чувствительны), чем их параметрические конкуренты, и если важно обнаружить даже слабые отклонения, следует особенно внимательно выбирать статистику критерия.
В нашей задаче с резервуарами можно применить тест Стьюдента для двух независимых выборок. Второй альтернативой является универсальный инструмент – бутстрэп.
Бутстрэп
Это один из самых интересных способов оценки метрик в А/Б-тестах, мы с удовольствием используем его в Retail Rocket для непрерывных параметров, таких как стоимость средней покупки, средняя стоимость товара, средний доход на посетителя сайта (Revenue per Visitor, RPV).
Бутстрэп [79] (оригинальная статья) работает за счет многократных выборок из данных, по которым затем считаются статистики. Алгоритм выглядит следующим образом [80]:
1. Необходимо задать количество выборок, которые мы сделаем из исходного датасета. Само число должно быть не меньше сотни. Больше – лучше.
2. При каждом повторении выборки (их всего будет) из исходного датасета случайно выбираются элементы с замещением, столько же, сколько было в исходном датасете (для сохранения вариации параметра [81]). В этой процедуре некоторые элементы исходного датасета будут выбраны несколько раз, некоторые – никогда.
3. Для каждой выборки вычисляется нужный нам параметр.
4. Теперь у нас есть k значений, которые можно использовать для вычисления доверительного интервала или статистического теста.
В А/Б-тестах мы работаем с двумя группами – контрольной и тестовой. По каждой группе нужно сделать свой бутстрэп. Считаем в каждой выборке и группе необходимую метрику. Для каждой выборки считаем разность метрик между группами. Таким образом мы получим k значений распределения разности в двух группах. Для вычисления значимости А/Б-теста нулевая гипотеза H0 формулируется так: две выборки одинаковы, поэтому разность между ними равна нулю. Если уровень нашей ошибки первого рода = 0.05, тест двусторонний, то нам просто нужно вычислить перцентили (квантили) для отрезка [/2, 100 % – /2], то есть [2.5 %, 97.5 %]. Это легко сделать самостоятельно, если отсортировать наш ряд значений разницы метрик и определить значения перцентилей на концах. Если 0 будет находиться между двумя этими значениями, то нулевую гипотезу отвергнуть нельзя, если вне – отвергаем.
Вспомним наш пример с двумя резервуарами, у нас есть выборки по 1000 шаров из каждого. Напомню, что в задаче мы должны ответить на вопрос, есть ли разница в среднем диаметре шара между резервуарами. Для процедуры бутстрэпа делаем k = 300 выборок для обеих групп, сразу считаем среднее в каждой выборке и разность между ними. В итоге мы получим 300 чисел. Сортируем по убыванию и выбираем два числа – одно на 2.5-й перцентиле (2.5 % × 300 = 7.5 или на 7 позиция), второе на 97.5-м перcентиле (97.5 % × 300 = 292.5 или 293-я позиция). Если оба числа оказались или положительными, или отрицательными, значит, разница статистически значима.

