Само слово «бутстрэп» произошло от выражения «To pull oneself over a fence by one’s bootstraps» (перебраться через ограду, потянув за ремешки на ботинках) – практически то же самое сделал барон Мюнхгаузен, когда вытянул сам себя за волосы из болота. Сейчас бутстрэпом называют такое «самовытягивание», когда мы получаем что-то бесплатное и полезное.
Плюсами бутстрэпа являются: независимость от распределения выборки, отсутствие параметров, кроме количества выборок, возможность легко подсчитать любую метрику. К минусам бутстрэпа относится очень высокая вычислительная требовательность. Создание тысяч выборок требует больших ресурсов. Третья альтернатива для А/Б-тестов – байесовская статистика.
Байесовская статистика
Впервые я познакомился с байесовским подходом для A/Б-тестов, когда прочитал статью Сергея Фельдмана на сайте нашего конкурента Richrelevance про этот тип тестов [82]. Одним из аргументов в пользу байесовских тестов для меня было сравнение двух формулировок итогов A/Б-тестов:
• мы отклоняем нулевую гипотезу, что A = Б, с p-значением 0.043;
• с 85 %-ной вероятностью А лучше Б на 5 %.
Первая формулировка принадлежит традиционной фишеровской статистике, вторая – байесовской. В статье [82] Сергей обращал внимание на следующие два недостатка p-значений для работы с гипотезами:
P-значение – сложная концепция, ее приходится каждый раз объяснять. Что касается меня, то я был хорошо знаком с ней еще в 2002 году. Периодически мне приходится напоминать себе о ней, и тогда я обращаюсь к литературе.
P-значение использует бинарный подход – мы или оставляем нулевую гипотезу или отвергаем ее, сравнивая p-значение со значением = 0.05.
Классическая математическая статистика (frequentist approach) относится к параметру как к фиксированной неизвестной константе. Байесовская статистика относится к параметру как к вероятностной величине [83]. Это чем-то похоже на разность в подходах классической и квантовой физики. Мне лично больше нравится вероятностный подход байесовской статистики, он выглядит нагляднее и естественнее, чем p-значение. Меня он так заинтересовал, что я долго искал хорошую и понятную литературу по этой теме. Очень полезной книгой оказалось «Введение в байесовскую статистику» [83] Уильяма Больстарда. Я очень ценю хорошие книги и могу назвать автора Учителем с большой буквы. Больстард очень хорошо выстроил систему вывода формул и доказательств. Я прочитал его книгу от корки до корки, решил почти все задачи в ней и написал первую версию программной библиотеки для A/Б-тестирования в Retail Rocket. Читая книгу Антонио Рохо о Рональде Фишере [76], я обнаружил интересный факт про байесовскую статистику – оказывается, она широко использовалась для оценки статистической значимости еще в дофишеровскую эпоху. Сторонники традиционного статистического подхода Фишера и сторонники байесовского подхода спорят до сих пор, какой метод лучше.
Сам преподобный Байес написал формулу так:
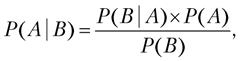
где:
P (A) – априорная информация, которая говорит о наших предположениях до проведения эксперимента. Это наши убеждения (может быть, даже интуитивные) до проведения эксперимента.
P (A | B) – апостериорная вероятность, когда формула суммирует убеждения (P (A)) до эксперимента и данные B, приводя к новым выводам, которые называются апостериорными.
P (B | A) – (likelihood) вероятность наступления события B при истинности гипотезы A.
P (B) – полная вероятность наступления события B.
Формула Байеса позволяет «переставить причину и следствие»: по известному факту события вычислить вероятность того, что оно было вызвано данной причиной. Для оценки параметров формулу можно переписать в другом виде:
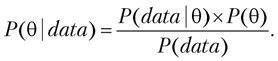
Мы хотим получить распределение параметра (например, среднего диаметра шара) после получения данных (data) в нашем эксперименте, при этом до эксперимента мы считаем, что наш параметр подчиняется распределению P(). В [83] указаны все выкладки для биномиальных тестов, например, когда мы сравниваем конверсию посетителя в покупателя. Так и для непрерывных нормально распределенных величин, когда мы можем сравнить средний диаметр шаров в наших резервуарах или средний чек в экспериментах на интернет-магазинах. Обе эти задачи относительно легко считаются, так как там используются сопряженные (conjugate) распределения. Для расчета А/Б-теста нужно воспользоваться постериорными формулами и применить сэмплирование, это очень похоже на то, что мы делали в бустрэпе.
Важная проблема в байесовской статистике – это выбор априорного суждения, именно к ней имеет претензии классическая статистика. У априорной информации есть свой «вес» (n equal sample size), выраженный в количестве точек данных. В той же книге есть также формулы для оценки «веса» априорных распределений, выраженных в количестве точек данных. Изучая литературу, я вывел для себя следующие правила. Если ничего не знаешь – используй равномерное (uniform) распределение. Если знаешь – то лучше использовать нормальное распределение, где априорное среднее – это ваше предположение, а априорное стандартное отклонение характеризует вашу уверенность в нем. «Вес» вашей уверенности лучше оценить по формулам во «Введении в байесовскую статистику» [83] – тогда вы будете понимать, сколько данных вам понадобится, чтобы изменить точку зрения. Я предпочитаю уверенность делать меньше, чтобы эксперимент быстрее сошелся. Ваши априорные суждения можно представить себе как увеличительное стекло, которое сфокусировано в точке вашей уверенности. Если данные не будут ее подтверждать, то фокус сам сместится ближе к правильному решению. Если подтвердят, то тест сойдется быстрее, так как фокус находился в нужном месте, вы не ошиблись. Например, когда тестируются разные версии рекомендательных алгоритмов, чтобы проверить, улучшилась ли конверсия посетителей в покупателей, вы можете смело взять текущую цифру конверсии (до эксперимента) в качестве априорного среднего. Априорное стандартное отклонение не стоит делать очень узким.
Второй проблемой байесовской статистики является привязка к распределению исходной величины – оно должно быть вам известно. В этом плане бутстрэп лучше, но считается он гораздо дольше, чем байесовский метод.
А/Б-тесты в реальности
Я уже расписал основные плюсы и минусы алгоритмов тестирования. Более подробные советы можно найти в книге «Семь главных правил экспериментов на веб-сайтах» [84]. Хочу предупредить читателя: к сожалению, в интернете много советчиков-теоретиков (и даже целые школы), которые все очень усложняют. Но даже научные статьи порой изобилуют ошибками, особенно если не были опубликованы в научных журналах и не озвучивались на авторитетных научных конференциях. Что уж говорить про посты уважаемых блогеров. Я сторонник простоты и считаю, что в методиках тестирования и анализа можно разобраться самостоятельно. Просто начинать нужно с самого простого – с фишеровской статистики с p-значениями. Открою секрет – если ваш тест действительно значим и данных в выборках достаточно, то все три метода покажут статистическую значимость. А вот ошибки, с которыми я сталкивался:

