Гвен. Поэтому r равно квадратному корню из двух! Это и есть секретное соотношение, которое положит конец всем мучениям и объединит человечество!
Свен (внезапно с другим акцентом). Прекрасно, Гвен. Уступи мне это число.
Гвен. Свен? Зачем ты достал пистолет?
Я заблуждался: создатели формата А4 выбрали соотношение сторон не для того, чтобы насолить лично мне. Они выбрали его и не по сиюминутному капризу, и не в знак упорного противостояния американской гегемонии, и не из садистского удовольствия подобрать иррациональное число.
На самом деле они его в принципе не выбирали.
Они решили создать систему бумажных форматов, каждый из которых вдвое меньше предыдущего. Это довольно крутой и труднодостижимый трюк. Но когда они вступили на этот путь, решение перестало зависеть от их выбора. Есть всего одно число, отвечающее поставленным требованиям, и так уж вышло, что это и есть знаменитое иррациональное число
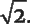
Теперь я знаю, что всем нам нравится воображать дизайнеров бумаги необузданными фантазерами, ограниченными только пределами своего воображения. Но в действительности все намного интереснее. Дизайнеры движутся в пространстве возможностей, которыми управляют логика и геометрия. Это застывший ландшафт: некоторые числа рациональны, другие нет, и ни один дизайнер ничего не может тут поделать. Вместо этого он должен лавировать среди этих препятствий — или, что даже лучше, превратить их в преимущества, как архитектор, чье здание гармонирует с окружающей средой.
Короче говоря, не буду долго разглагольствовать: я поменял свое мнение о формате А4. Теперь, когда я знаю, почему соотношение сторон стремится к
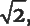 тот факт, что производители бумаги обречены на микроскопическую ошибку, меня больше не тревожит. Честно говоря, формат А4 даже перестал казаться мне неправильным. Теперь меня, наоборот, раздражает бумага формата US Letter, слегка располневшая и старомодная.
тот факт, что производители бумаги обречены на микроскопическую ошибку, меня больше не тревожит. Честно говоря, формат А4 даже перестал казаться мне неправильным. Теперь меня, наоборот, раздражает бумага формата US Letter, слегка располневшая и старомодная.
Кажется, я завершил переход из одной категории несносных американцев в другую. Из шовиниста и поборника моих своевольных национальных обычаев я стал страстным проповедником зарубежных традиций. Сейчас я даже реже пью карамельные коктейли, хотя уверен, что полностью никогда не откажусь от них, как и от бумаги американского формата.
Глава 8. Квадратно-кубические басни
Простые сказки о математическом масштабировании
У басен много общего с математикой. И те и другие пришли из пыльных, изъеденных молью книг. Их навязывают детям. И они пытаются объяснить мир с помощью радикальных упрощений.
Если вы хотите познакомиться со всей причудливостью и сложностью жизни, оглядитесь вокруг. Поговорите с биологом, или художником-реалистом, или с кем-нибудь, кто собирает документы для уплаты налогов. Баснописцы и математики скорее сродни карикатуристам. Педалируя одни черты и пренебрегая всеми остальными, они помогают объяснить, почему наш мир таков, каков он есть.
Эта глава — небольшое собрание математических басен. Они показывают, как разные области, от кулинарии до биологии и финансирования искусства, подчиняются законам геометрии. В основе этих басен лежит одна основная идея, мораль настолько простая, что даже Эзоп не проговаривал ее вслух: размер имеет значение
[42].
Большая статуя — не просто увеличенная версия маленькой статуи. Это совершенно иной объект.
1. Почему шоколадные торты лучше печь в больших формах
Мы с вами любим печь торты. Мы с гордостью месим тесто, чтобы осчастливить человечество шоколадным чудом. Духовка уже нагревается, но когда мы открываем кухонный шкаф, то неожиданно обнаруживаем, что наша форма для выпечки в два раза длиннее и шире, чем указано в рецепте из поваренной книги
[43].
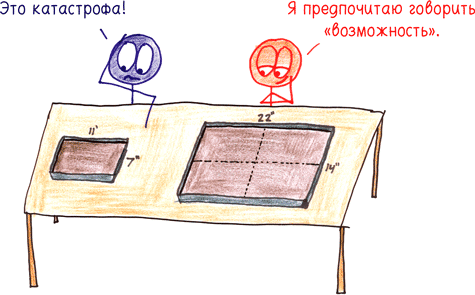
Что же нам делать?
Для того чтобы заполнить эту удвоенную форму для выпечки, у нас есть искушение взять в два раза больше ингредиентов. Но на самом деле это полумера. Посмотрите внимательнее, и вы поймете: нам необходимо учетверить количество ингредиентов.
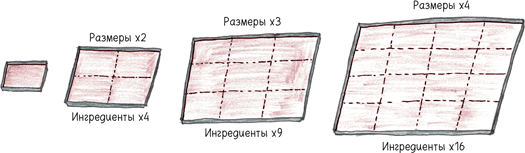
С какой стати? Но ведь у формы два измерения: длина и ширина. Удваивая длину, мы удваиваем площадь формы. Удваивая ширину, мы снова удваиваем площадь. Таким образом, площадь удваивается дважды. Иными словами, умножается на 4.
Так происходит всякий раз, когда вы увеличиваете прямоугольник. Утраиваете стороны? Площадь возрастает в девять раз. Упятеряете стороны? Площадь возрастает в 25 раз. Умножаете стороны на девять тыщмиллионов? Площадь увеличивается в 81 тыщмиллионов тыщмиллионов раз.
Или, говоря точнее: увеличивая стороны в r раз, вы увеличиваете площадь в r2 раз.
Так происходит не только с прямоугольниками. Тот же принцип работает для всех двумерных фигур: трапеций, треугольников, кругов и других емкостей, в которые вы укладываете заветное шоколадное тесто. Когда стороны увеличиваются, площадь увеличивается существенно больше.
Вернемся на кухню. Мы уже смешали вчетверо большее количество ингредиентов, когда на дальней полке обнаруживаются формы, которые мы искали все это время. Мы осыпаем друг друга упреками, но потом смеемся: кому охота пререкаться, когда скоро будет готово шоколадное великолепие?
Теперь перед нами встает выбор: готовить торт в одной большой форме или в четырех поменьше?
Это басня, поэтому мы пренебрегаем деталями. Забудьте о температуре, времени приготовления, теплопередаче и предстоящем мытье посуды. Сосредоточьтесь на одном параметре: размерах форм для выпечки.



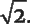
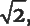 тот факт, что производители бумаги обречены на микроскопическую ошибку, меня больше не тревожит. Честно говоря, формат А4 даже перестал казаться мне неправильным. Теперь меня, наоборот, раздражает бумага формата US Letter, слегка располневшая и старомодная.
тот факт, что производители бумаги обречены на микроскопическую ошибку, меня больше не тревожит. Честно говоря, формат А4 даже перестал казаться мне неправильным. Теперь меня, наоборот, раздражает бумага формата US Letter, слегка располневшая и старомодная.
