

Третий подход: перенумеровать грани
[62]. У обычной игральной кости сумма чисел на противоположных гранях равна семи. (Пары 1 и 6, 2 и 5, 3 и 4.) В игральных костях под названием «чечетка» (taps) некоторые числа продублированы, и на противоположных гранях расположены 6 и 6, 5 и 5, 4 и 4. С любого ракурса ваш противник будет видеть всего три грани, поэтому не заметит подвоха
[63].
Хотя подобные мошеннические методы нацелены на игральные кубики, эта форма игральных костей не самая уязвимая. Просто самая популярная. Очевидно, что в крэпс можно выиграть больше денег, чем в «Подземелья и драконы».

Правило № 6. Хорошая кость — наш вечный гость
Суть игры в кости, как и многих других игр, состоит в том, что в ней нет никакой необходимости. Мы живем в XXI веке. Я добираюсь на работу с помощью реактивного ранца и улетаю в отпуск на крылатом автомобиле. Ладно, я пошутил, но зато я ношу в кармане полмира в виде 140-граммового компьютера. Технологии делают всех нас устаревшими, в том числе работяг, которых называют игральными костями. Смотрите: я хочу оторваться от этого текста и смоделировать миллион бросков игрального кубика в Microsoft Excel. Я дам вам знать, сколько времени это займет.
Окей, готово. Потребовалось около 75 секунд. Вот результаты:
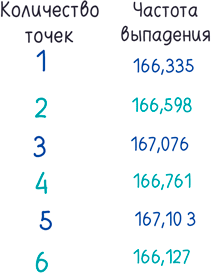
Мало того, что компьютерная генерация случайных чисел быстрее и проще, чем кидание пластикового кубика на стол, она еще и подразумевает более высокую степень случайности. Владельцы казино могут выбросить все рулетки и столы для крэпса: их цифровые заменители будут опережать доисторические генераторы случайных чисел семимильными шагами.
Но разве это будет весело?
Игральные кости созданы для того, чтобы трогать их руками. Первый раз, когда я сыграл в «Подземелья и драконы» (на самом деле первый и последний), я увидел кое-что более завораживающее, чем все орки и маги: зоккиэдр, стогранную игральную кость. Представляете? Сто граней! Игральная кость, которая катится полминуты, прежде чем остановиться! Я знал, что две десятигранные игральные кости (одна для десятков, другая для единиц) удобнее для игры и честнее, чем бритый бугорчатый мячик для гольфа Лу Зокки. Но мне было все равно. Я хотел кидать этот стогранник
[64].

Древние греки, должно быть, чувствовали тот же соблазн, когда кидали надпяточную овечью кость под названием астрагал. Они нумеровали четыре грани странным образом (1, 3, 4 и 6) и бросали пригоршню костей. Единица называлась «псы»: худшее, что можно себе вообразить. Лучший исход назвался «Афродита» (шестерка или другая грань, смотря кого вы спросите). Астрагалы не были честными; они были лучше. Это были частицы скелета в человеческой руке, предсказывающие судьбу. Когда Юлий Цезарь пересек Рубикон, рубеж между закатом Римской империи и зарей Римской республики, он сказал: «Alea iacta est». Жребий брошен.
Игра в кости, я так подозреваю, никогда не исчезнет. Эти кости вошли в нашу плоть и кровь. Просто следуйте этим шести правилам:
Хорошая кость
играет честно,
выглядит прелестно,
работает повсеместно,
ее легко кидать,
но сложно в узде держать.
Хорошая кость —
наш вечный гость.
Глава 10. Устная история «Звезды смерти»
Воспоминания о самом знаменитом шаре в галактике
Вероятно, величайший конструкторский проект в истории геометрии — «Звезда смерти». Она была чистейшим ужасом, пока ее не разрушил белокурый юноша из пустыни в трагическом финале фильма «Звездные войны»
. Она была исключительно красива. Почти идеальный шар, 160 км в поперечнике, оснащенный лазером, испепеляющим планеты. Но даже этот левиафан, спроектированный, чтобы держать в повиновении целую галактику, в свою очередь, повиновался более могущественному властелину — геометрии.
Геометрия не склоняется ни перед кем, даже перед империями зла.
Я собрал команду, ответственную за создание «Звезды смерти», чтобы обсудить геометрию самой спорной конструкции в истории
[65]. Они затронули несколько аспектов, связанных с постройкой огромной шарообразной космической станции:









