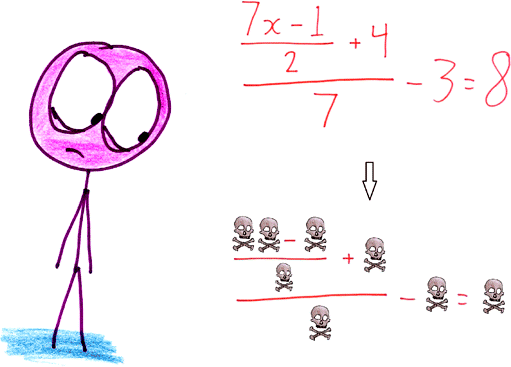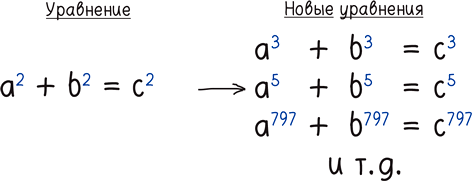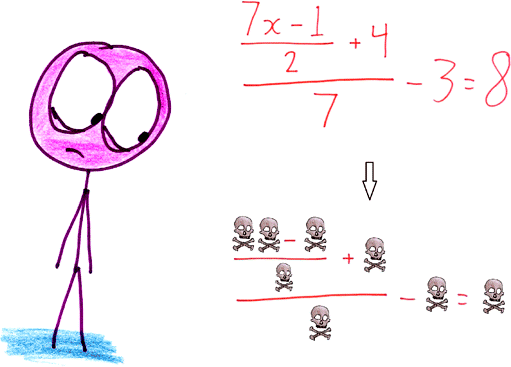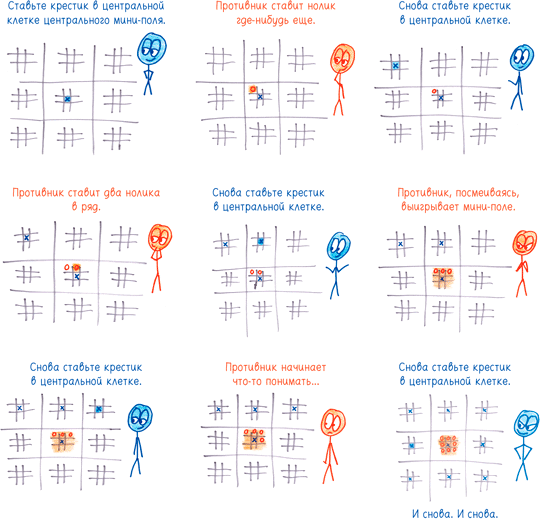
Иными словами, крестики жертвуют центральным мини-полем ради выигрышной позиции на оставшихся восьми. Я полагал, что эта стратегия весьма крута, пока читатели не указали мне на ее глубочайшую глупость. Гамбит Орлина дает небольшое преимущество, но его легко расширить до гарантированно беспроигрышной стратегии
[6]. Вы можете пожертвовать не одним мини-полем, а двумя, завоевав при этом по два крестика на одной прямой на оставшихся семи мини-полях.
Я был смущен и переформулировал старое правило — легкая перенастройка, которая вдохнула в жесткие крестики-нолики новую жизнь.
Новое правило — новая игра.
Именно так развивается математика. Мы выбираем правила и начинаем играть. Когда игра нам приедается, мы меняем правила. Мы вводим новые ограничения и смягчаем старые. Каждое нововведение влечет за собой новые головоломки и вызовы.
По большей части математики не бьются над чужими загадками, а изобретают свои собственные, исследуя, какие ограничения приводят к интересным играм, а какие — к наводящим скуку. В конце концов постоянная смена правил и перескоки от одной игры к другой становятся похожи на отдельную грандиозную нескончаемую игру.
Математика — это логическая игра по изобретению логических игр.
Вся история математики снова и снова иллюстрирует этот тезис. Логические головоломки изобретают, решают и изобретают снова. Например, что произойдет, если я подправлю знакомое уравнение и заменю двойку на другое число: 3, или 5, или 797?
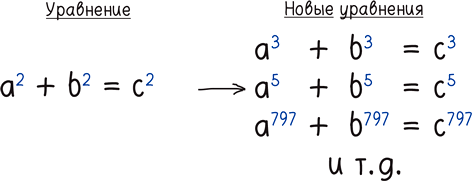
С ума сойти! Я превратил элементарное древнее уравнение, имеющее множество решений в целых числах (например, 3, 4 и 5), в самую досадную задачу, с которой когда-либо сталкивалось человечество, — в великую теорему Ферма. Она тревожила умы математиков около 350 лет, но в 1990-е годы гениальный британец
заперся на чердаке и вышел примерно десять лет спустя, щурясь на солнечный свет, с доказательством, что уравнение не имеет целочисленных решений, если степени неизвестных больше двух
[7].
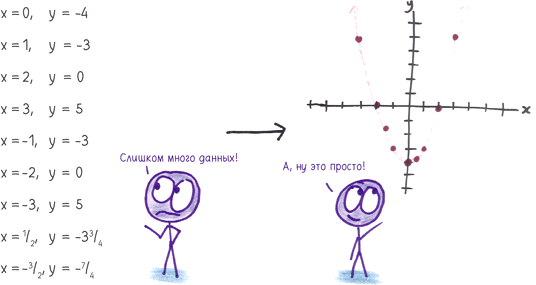
А что произойдет, если я возьму две переменных, скажем x и y, и построю координатную сетку, чтобы посмотреть, как они зависят друг от друга?
Невероятно! Я изобрел координатную плоскость и совершил революцию в математике, наглядно изобразив алгебраические идеи, и поэтому мне платят кучу денег. Будем знакомы: меня зовут Декарт.
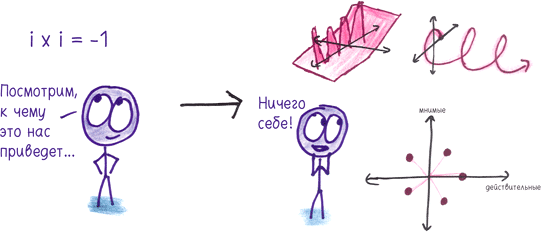
Или припомним, что возведение числа в квадрат всегда дает положительную величину. А что, если мы придумаем особое число, которое при возведении в квадрат дает отрицательную величину? И что тогда?
Вот это да! Мы изобрели мнимые числа, открыв возможности для исследования электромагнетизма и взломав математическую истину под названием «основная теорема алгебры»
. Звучит неплохо, можно включить в резюме.
В каждом из этих случаев математики поначалу недооценивали преображающую силу смены правил. Ферма полагал, что его теорема доказывается крайне просто; как выяснилось, он заблуждался, и его сбитые с толку преемники бились над доказательством несколько веков. Идея Декарта о координатной плоскости (которую называют «декартовой системой координат» в его честь) вначале была высказана в приложении к философскому тексту
; впоследствии текст забылся, а идея получила свое развитие. Над мнимыми числами издевались и смеялись несколько веков («настолько же неуловимые, насколько бесполезные», сказал великий итальянский математик Кардано
[8]), пока их не признали настоящими и полезными. Кстати, само слово «мнимый»
по отношению к таким числам изначально имело уничижительный смысл, и придумал это поношение не кто иной, как Декарт.
Легко недооценить новаторские идеи, если они родились не в результате серьезных размышлений, а во время игры. Кто мог предположить, что небольшая перемена в правилах (новая степень, новая визуализация, новое число) превратит фантазию в нечто официально признанное?
Не думаю, что математики на том пикнике думали о таких вещах, когда склонились над игрой в жесткие крестики-нолики. Но в этом и не было необходимости. Осознаём мы это или нет, но логическая игра по изобретению логических игр оказывает влияние на всех нас.
Глава 2. Как математику видят школьники?
Увы, эта глава будет краткой и мрачной. Я прошу прощения. Но я слишком занят, чтобы просить прощения даже за другие вещи, например за мои душеразжижающие уроки математики.
Вы понимаете, что я имею в виду. Для множества школьников заняться математикой означает записать карандашом предписанную последовательность действий. Математические символы ничего не символизируют; они просто пляшут по странице, выполняя бестолковые хореографические упражнения.
Вся эта математика, приятель, —
Побасенки и выдумки абака,
Сплошь синусы да греческие буквы,
Не значащие ровно ничего
.