
Эта формула фиксирует связь между двумя ипотечными кредитами с помощью одной-единственной величины: коэффициента корреляции в диапазоне от –1 до 1.
Копула — изящная часть математики, простая и элегантная, и это делает ей честь. Но на самом деле глобальная экономика далека от простоты, и в ретроспективе легко увидеть, что упускает копула (и подобные ей методы).
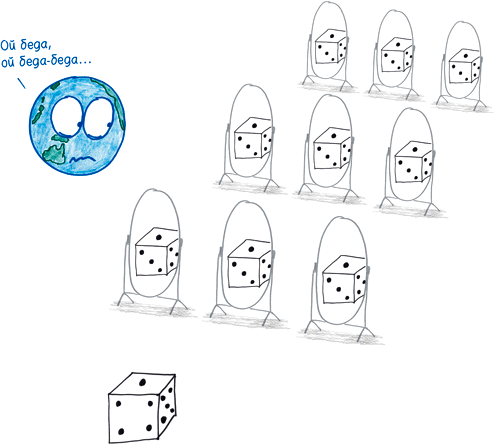
Во-первых, данные. Компьютеры Уолл-стрит жадно проглотили электронные таблицы с ценами на жилье. Но большинство данных из разных городов относилось к одному недавнему периоду, на протяжении которого (так уж вышло) цены на жилье, к радости банкиров, неуклонно росли. Модели откалибровали свои прогнозы, как будто бы они анализировали всю историю цен на жилье в США. На самом деле они стали свидетелями миллиона отражений одного броска игральной кости.
Во-вторых, модель была построена для пар событий (отсюда термин «копула» — «связка» по-латыни). Но дома не выстроены парами. Все вместе они составляют один общенациональный рынок. Одно изменение может одновременно повлиять на каждую ипотеку в стране — именно это произошло, когда взлетающий рынок грохнулся оземь. Глупо тревожиться, что одна костяшка домино повалит соседнюю, когда над всеми ними нависает одна гигантская костища.
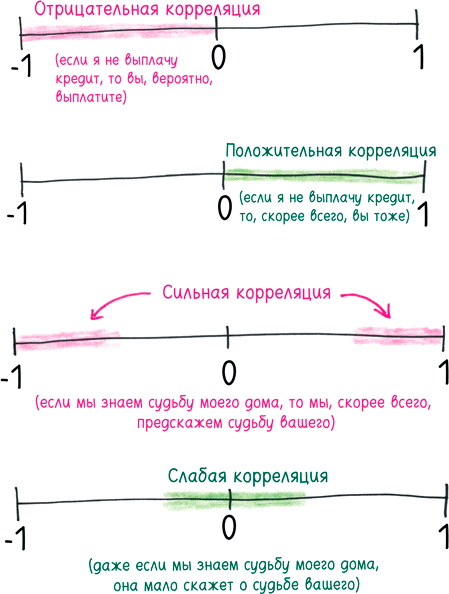
Наконец, если вы хорошо затвердили лексикон математической статистики, тревожный звоночек раздается при слове «гауссова». В математике этот термин возникает всякий раз, когда вы рассматриваете большую совокупность независимых событий. Но вся проблема в том, что в данном случае события зависят друг от друга.
По этим трем причинам на Уолл-стрит упустили из виду риск, который заметил Магритт, и это привело к стихийному бедствию, столь же сюрреалистичному, сколь все его фантазии. И мы все еще не обсудили худшее из всего этого. Неправильно оцененные CDO составляли несколько триллионов долларов — достаточно, чтобы нанести ущерб экономике, но недостаточно, чтобы объяснить жесткий нокаут в сентябре 2008 года. Почему экономика как подкошенная рухнула на ринг и выплевывала окровавленные зубы, ошеломленная подлым ударом? Это был провал теории вероятностей в еще большем масштабе.

4. Ставка 60 триллионов долларов — удваиваем или обнуляем?
Если вы освоили предыдущую главу (увеселительное чтение для всей семьи), то знаете, что страхование целесообразно. Я не могу позволить себе потерять родной дом (иначе куда будут приезжать курьеры с пиццей?), поэтому готов платить небольшие ежемесячные взносы ради крупной компенсации в том случае, если мой дом когда-нибудь сгорит. Я избегаю экзистенциального риска, страховая компания получает прибыль. Все в выигрыше.
Но мне приходит в голову странная идея. Что, если вы тоже купите страховку на мой дом?
Вы можете повторить мою сделку. Небольшие регулярные платежи возвратятся сторицей, если разразится катастрофа. Это бесцельное дублирование финансовой структуры страхования. Это просто пари, игра с нулевой суммой. Если мой дом сгорит, вы выиграете; если он будет оставаться в целости и сохранности, выиграет страховая компания. Еще более странная мысль: что, если тысячи людей сядут в этот вагон и купят страховку на мой дом в надежде выиграть, если он сгорит?

Я лишусь покоя, если буду получать анонимные подарки наподобие дешевых петард и боевых гранат. Но в этом сценарии я не единственный, кто будет страдать бессонницей; сотрудники страховой компании затрясутся от страха еще сильнее. Если мой дом сгорит, у них останутся лишь пригоршни пепла, потому что крупную компенсацию придется выплачивать в тысячекратном размере.
Поэтому ни одна страховая компания не заключит таких контрактов. Игра не стоит свеч: возможность легко извлечь прибыль с вероятностью 95 % перестает быть заманчивой, если в оставшихся 5 % случаев вас ожидает полнейший крах.
Жаль, что никто не рассказал об этом банкирам с Уолл-стрит.
Знаком злого рока для Уолл-стрит стала трехбуквенная аббревиатура: CDS, то есть кредитный дефолтный своп (credit default swap)
[138]. По сути дела, это страховые полисы CDO. Вы регулярно вносите скромные взносы. Пока проценты по CDO выплачиваются исправно, все остается как есть. Но если платежи по определенному числу ипотечных кредитов перестают поступать, CDS приносит вам кругленькую сумму.
Пока что все разумно. Но угадайте: что Уолл-стрит стала делать дальше? Там стали продавать десятки CDS на каждый базовый CDO. Похоже на продажу десятков страховых полисов на один и тот же дом, но с большим количеством нулей на конце итоговых сумм. К началу 2008 года на кону оказалось в общей сложности $60 трлн — примерно столько же, сколько составляет объем ВВП планеты Земля.
Краткое резюме. CDO подразумевали стабильную модель с миллионом игральных костей; вместо этого сработала непредсказуемость броска одной-единственной игральной кости. Ставки по CDS удваивались до тех пор, пока эта рискованная игра не поставила под удар всю мировую экономику. Возникает естественный вопрос:
Как Уолл-стрит могла свалять такого дурака?
[139]
Вы нанимаете величайшие умы из самых модных университетов, покупаете им суперкомпьютеры за миллионы долларов, платите им астрономические зарплаты, заставляете их работать по 90 часов в неделю… а потом заходите в офис и обнаруживаете, что они верещат и втыкают столовые вилки в электророзетки?







