5. Процентное изменение
Как вычислить? Прежде чем сообщить, насколько изменилась величина, поделите эту разницу на исходное значение.
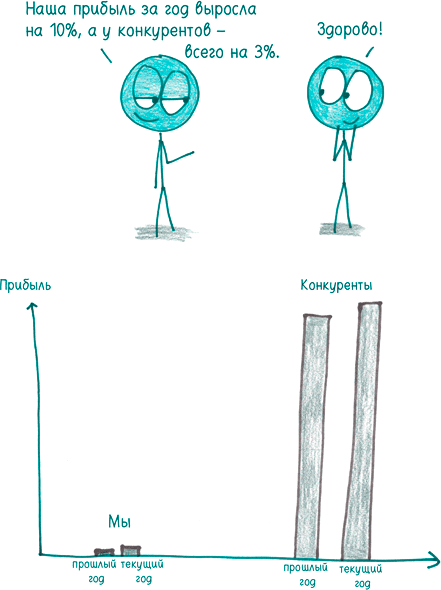
Когда использовать? Процентное изменение позволяет посмотреть на вещи в перспективе. Оно определяет прибыли и убытки как части целого. Скажем, моя прибыль составила $100. Если вначале у меня было всего $200, то этот золотой дождь обеспечил рост капитала на 50 %, и я прыгаю от счастья и виляю хвостом, как Снупи. Но, если у меня уже было $20 000, рост моего дохода составляет всего лишь 0,5 %; я ограничиваюсь тем, что вскидываю вверх кулак. Перспектива имеет решающее значение, когда вы наблюдаете рост величины с течением времени. Если бы 70 лет назад американцы услышали, что наш ВВП за год вырос на $500 млрд, они испытали бы благоговейный трепет. Если бы они узнали, что рост составил 3 %, они бы не сильно удивились.
Почему нельзя доверять? О, я всецело за взгляд в перспективе. Но процентное изменение, пытаясь обеспечить контекст, может его, наоборот, уничтожить. Когда я жил в Великобритании, вкусный томатный соус по два фунта за банку иногда продавался со скидкой — в два раза дешевле
[145]. В эти дни я как будто выигрывал джекпот: 50 % экономии! Я волок домой дюжину банок — можно заправлять равиоли целый месяц. Вскоре меня пригласили на свадьбу в США. За неделю авиабилеты могли подскочить в цене на 5 %. «Ну и ладно, — сказал я, соглашаясь на повышенную цену. — Это ненамного больше».

Вы понимаете проблему: из-за инстинктов у меня оказалось на пенни ума и на фунт глупости. «Огромная» скидка сэкономила мне 12 фунтов, в то время как «незначительный» рост цен на авиабилеты стоил мне 30 фунтов. Деньги есть деньги, будь то счет в овощной лавке на $20 или ипотека в $200 000. Большие процентные скидки на дешевые товары — ерунда на фоне нескольких процентов подорожания дорогих вещей.
6. Диапазон
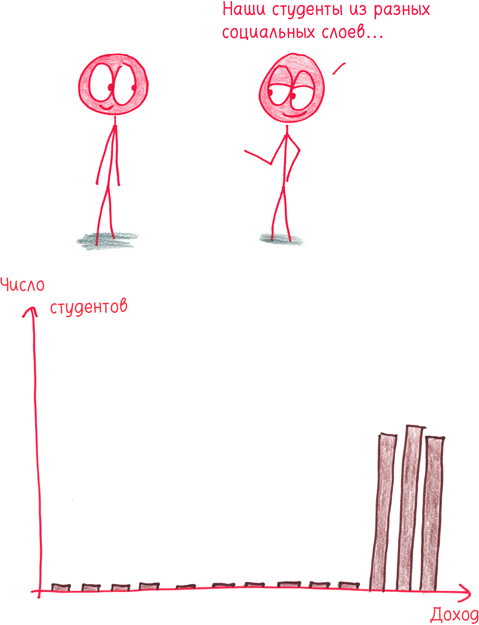
Как вычислить? Диапазон — это разница между наибольшей и наименьшей величиной.
Когда использовать? Среднее арифметическое, медиана и мода имеют дело с основной тенденцией: они сводят все разнообразие набора данных до одного репрезентативного значения. Диапазон преследует противоположную цель: не замести разногласия под ковер, а вычислить и показать их, чтобы измерить разброс данных. Заслуга диапазона в его простоте. Мы воспринимаем набор данных как спектр от наименьшего к наибольшему и выясняем ширину этого спектра. Это быстрая и грубая оценка разнообразия.
Почему нельзя доверять? Диапазон учитывает только два куска пирога — наименьший и наибольший. Мы упускаем очень много важной информации, а именно размеры всех прочих кусков. Они близки к максимуму? Близки к минимуму? Распределены равномерно? Диапазон не знает и не хочет выяснять. Чем больше набор данных, тем сомнительнее становится смысл диапазона, потому что он игнорирует миллионы промежуточных значений, чтобы узнать о двух наибольших отклонениях. Узнай инопланетянин о двухметровом диапазоне роста взрослых людей (от рекордно низких 60-сантиметровых до рекордно высоких — 274 см), он был бы крайне разочарован, посетив Землю и выяснив, что все мы уныло средние — примерно от 152 до 183 см.
7. Дисперсия (и среднеквадратичное отклонение
)
Как вычислить? Среднеквадратичное отклонение показывает, грубо говоря, насколько далеко типичная величина из набора данных отстоит от среднего арифметического.
Если вы хотите приготовить дисперсию у себя на кухне, воспользуйтесь следующим рецептом: (1) найдите среднее арифметическое вашего набора данных; (2) вычислите, насколько далеко каждая величина отстоит от среднего арифметического; (3) возведите эти разности в квадрат; (4) найдите среднее арифметическое квадратов разностей. Среднее арифметическое квадратов отклонений от среднего арифметического и есть дисперсия.

Если вы извлечете квадратный корень из дисперсии, вы получите «среднеквадратичное отклонение»
[146]. Это более естественная величина, поскольку дисперсия измеряется в странных единицах. (Что такое «доллар в квадрате»? Никому это не ведомо.)
Дисперсия и среднеквадратичное отклонение идут вместе рука об руку, поэтому мы обсуждаем их в одном параграфе.
Когда использовать? Как и диапазон, дисперсия и среднеквадратичное отклонение дают численное значение разброса величин в наборе данных, но (говорю со всей беспристрастностью любящего отца) они лучше. Диапазон — быстрая, сделанная на скорую руку оценка разброса; дисперсия — несущая опора статистики. Дисперсия учитывает вклад каждой величины из набора данных и достигает сложности симфонии, в то время как диапазон бренчит на двух струнах.
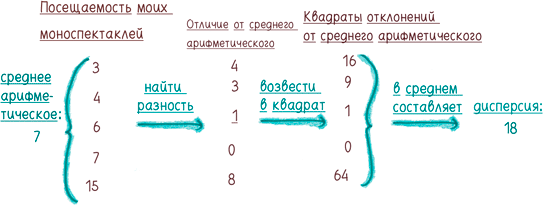
Логика дисперсии, пускай витиеватая, при ближайшем рассмотрении имеет смысл. Ключевую роль играет отличие от среднего арифметического. Большая дисперсия означает, что данные широко разбросаны; маленькая дисперсия означает, что они тесно жмутся друг к другу.
Почему нельзя доверять? Разумеется, дисперсия учитывает вклад каждой величины из набора данных. Но вы не можете сказать, кто вносит что.
Точнее говоря, одна далеко отстоящая величина может обеспечить взрывной рост дисперсии. Из-за возведения в квадрат одно значительное отклонение от среднего арифметического (например, 122 = 144) может внести больший вклад, чем дюжина небольших (например, 32 = 9; двенадцать девяток дают всего-навсего 108).







