Возьмем формулу S = πR2, которую многие школьники слышат так часто, что фраза «площадь круга» вызывает у них рефлекторное желание закричать: «Пи эр квадрат!» Они как агенты глубокого внедрения с промытыми мозгами. Но что значит эта формула? Почему это так?
Ладно, забудьте о числе 3,14159. Раскрепостите сознание. Просто поглядите на геометрические фигуры: r — это радиус круга, длина отрезка; r2 — это площадь квадрата (он изображен на чертеже). А теперь вопрос на π долларов: как площадь круга соотносится с площадью этого квадрата?
Очевидно, что площадь круга больше. Но не в четыре раза больше, потому что четыре квадрата покроют не только круг, но и дополнительную часть плоскости. Кроме того, присмотревшись, вы поймете, что площадь круга немного больше, чем площадь трех квадратов.
Это именно то, что утверждает наша формула: площадь круга чуть-чуть больше, чем 3 × r2.
Если вы хотите установить точное значение числа π (почему 3,14, а не 3,19?), вам придется прибегнуть к доказательству. (Есть несколько великолепных наглядных доказательств, мое любимое заключается в том, чтобы снимать с круга слой за слоем, как будто кожицу с луковицы, и в итоге получить многоугольник
[11].) Но математики, что бы они ни доказывали, не всегда исходят из первичных принципов. Как и представители других профессий, от плотников до смотрителей зоопарка, они с радостью используют какой-нибудь инструмент, даже не зная в точности, каким образом он сконструирован, до тех пор, пока у них есть ощущение, что он работает.
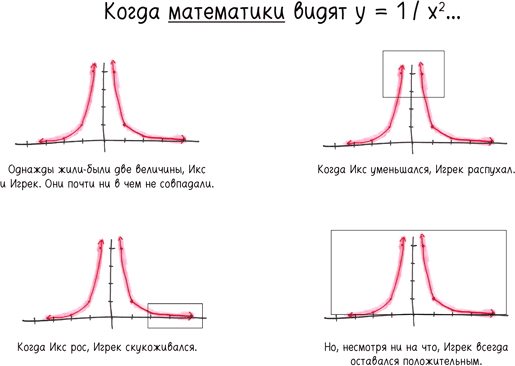
«Постройте график исходя из уравнения» — знакомое домашнее задание. Я и сам его задавал. Кроме того, это зародыш порочного мифа: якобы графики являются самоцелью. На самом деле их построение не похоже на решение уравнений или выполнение операций. График — это не конечный пункт, а всегда не более чем средство.
График — это способ визуализировать данные, картинка, которая рассказывает историю. Он представляет собой еще одну могущественную стратегию чтения математических текстов: превратить статику в динамику.
Возьмем уравнение, приведенное выше: y = 1/x2. Здесь x и y — пара взаимосвязанных чисел. Вот несколько примеров:
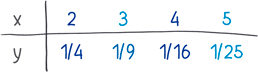
Уже просматривается несколько закономерностей. Но чем лучше наши технические приемы, тем больше мы видим, и таблицы — не модный инструмент. Из бесконечных пар x — y, которые подходят нашему уравнению, таблица, как бегущая строка биржевых индексов, может показать всего лишь несколько. Нам нужен инструмент визуализации получше: математический аналог телевизионного экрана.
На сцене появляется график.
Рассматривая x и y как своего рода широту и долготу, мы преобразуем каждую неосязаемую пару чисел в нечто геометрическое — точку. Бесконечное множество точек становится непрерывной кривой линией. И тогда возникает история, рассказ о движении и изменении.
• Когда x уменьшается, стремясь к нулю (1/5,1/60,1/1000…), y раздувается до немыслимых величин (25, 3600, 1 000 000…).
• Если x увеличивается (20, 40, 500…), y скукоживается до микроскопических чисел (1/400,1/16 000,1/250 000…).
• Когда x принимает отрицательные значения (–2, –5, –10), y остается положительным. Он никогда не спускается ниже нуля.
• Ни одна из величин не может быть равна нулю.
Окей, возможно, это не самая сочная сюжетная линия, но такие умственные упражнения показывают разницу между математиком-новичком (он видит парализующий поток бессмысленных символов) и опытным математиком (он видит нечто слаженное и дружелюбное). Графики наполняют безжизненные уравнения ощущением движения.
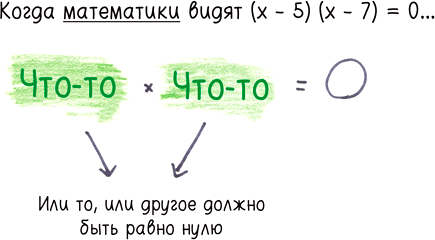
Есть психологический феномен, известный под неприятным названием чанкинг. Это не просто способ очистить организм после чрезмерного количества пива
, но и мощная ментальная техника, необходимая математикам. Очередная стратегия чтения математических текстов.
Чанкинг означает, что мы интерпретируем набор разрозненных, ускользающих деталей как единое целое. Приведенное выше уравнение — хороший пример. Умелый чанкер игнорирует мелочи слева. Там x или y, 5 или 6, плюс или минус? Не знаю, без разницы. Вместо этого вы видите просто два множителя, формирующих скелет уравнения: чанк умножить на чанк равно нулю.
Если вы знакомы с таблицей умножения, вы знаете, что ноль — это своеобразный результат.
6 × 5? Не ноль.
18 × 307? Не ноль.
19,91632 × 4 600 000 000 000? Нет смысла открывать калькулятор на вашем смартфоне: это тоже не ноль.
Ноль — единственное в своем роде число в мире умножения. В отличие от числа, скажем, 6, которое можно разложить на множители различными способами (3 × 2, 1,5 × 4, 1200 × 0,005…), ноль — особая, своенравная величина. На самом деле есть всего один способ получить ноль, перемножая два числа: если одно из них само по себе равно нулю.
Здесь окупается наша стратегия дробления: один из множителей равен нулю. Таким образом, x равен либо 5, либо 7.
Уравнение решено.
Чанкинг прочищает не только наши желудки, но и наши умы. Он делает мир удобоваримым. Чем больше вы узнаете, тем агрессивнее вы чанкаете. Старшеклассник может прочанкать целую строку алгебраических символов и понять, что это формула площади трапеции. Старшекурсник может прочанкать несколько дремучих строчек вычислений и увидеть, что это формула объема твердого тела вращения. Аспирант прочанкает полстраницы грозных греческих букв и сделает вывод, что речь идет о вычислении хаусдорфовой размерности множества. Чем выше ваш уровень, тем больше вы узнаете. Что такое трапеции? Как ведут себя интегралы? Что курил Хаусдорф
и где бы нам такое раздобыть?
Но мы не изучаем детали ради деталей. Мы узнаем детали, чтобы позже их проигнорировать и сосредоточиться на более общей картине.





