При реальном расчете угрозы СВДС факторы риска для каждой семьи не выбираются случайным образом из всего их многообразия; они уже заданы заранее – можно утверждать, что с самого начала вы либо выбираете из мешочка с черным шариком в нем, либо из другого, в котором черного шарика заведомо нет. Эта альтернативная интерпретация проиллюстрирована в виде двух деревьев принятия решений на рис. 10. Если вам достался мешочек с черным шариком в обоих случаях, то вероятность выбора двух черных шариков возрастает до 1 к 100. Таким образом очевидно, что простое перемножение общепопуляционного фактора фонового риска развития СВДС на самого себя при вычислении вероятности развития СВДС для конкретного случая – некорректный прием.
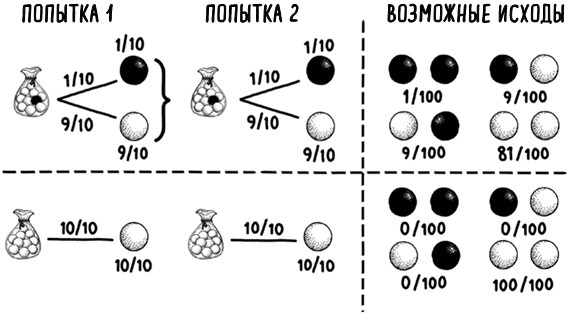
Рис. 10. Два альтернативных древа принятия решений, где мешочек, из которого вы выбираете, жестко задан заранее для обеих попыток выбора. Для каждого древа вероятность выпадения каждой из двухвариантных комбинаций выбора показаны справа от пунктирной линии. Очевидно, что если мы выбираем из мешочка, где черного шарика нет, то единственная возможность – это выпадение двух белых шариков
•
Тенденциозный подход Мидоу, опиравшегося на общий показатель 1 случай смерти от СВДС на 8543 случая живорождения, имел и другие слабые места. Отчет, из которого он выбрал этот показатель, предлагал и другую, гораздо более высокую общепопуляционную оценку риска – 1 к 1303 (этот показатель был рассчитан без разделения данных по социально-экономическим факторам). Мидоу решил не использовать эту альтернативную оценку. Вместо того, сделав особый акцент на условиях жизни семьи Кларк, Мидоу вывел значение, согласно которому вероятность даже одного случая СВДС выглядела гораздо ниже (а поскольку он безосновательно проигнорировал зависимость между серийными смертями от СВДС, повторная смерть от этого синдрома выглядела еще менее вероятной), пренебрегая теми факторами, которые делали его гораздо более вероятным. Так, он проигнорировал тот факт, что оба ребенка Салли были мальчиками и что СВДС у мальчиков развивается почти в два раза чаще, чем у девочек. Учет этого фактора подорвал бы позиции обвинения, показав более высокую вероятность серийной смерти от СВДС. В этом свете шанс, что Салли убила двух своих детей, представляется соразмерно ниже.
Хотя тенденциозный подбор стороной обвинения статистических данных сам по себе мог бы считаться неэтичным или даже заведомо ложным, подобная практика порождает куда более серьезную проблему. Классификация данных в докладе, на который опирался Мидоу, была проведена, чтобы выявить категории населения, наиболее подверженные высоким рискам и более эффективно использовать ограниченные ресурсы системы здравоохранения. Она никогда не предназначалась для того, чтобы делать выводы о риске развития СВДС в каждом конкретном случае – даже в этих группах повышенного риска. Доклад представлял собой самое общее исследование почти полумиллиона родов в Великобритании, а при таком исследовании индивидуальные обстоятельства каждых родов детально изучить невозможно (да и цели такой обычно не ставится). Дело же Салли Кларк, напротив, было чрезвычайно подробным расследованием конкретного случая. Обвинение выбрало только те аспекты биографии Салли и Стива, которые подходили под нарисованную в отчете картину, и, без учета других факторов, решило использовать эту конструкцию для определения степени риска развития СВДС у детей четы Кларк. Однако такой подход основан на ложном допущении о том, что индивидуальные характеристики тождественны характеристикам населения. Это классический пример так называемой экологической ошибки.
Экологическая ошибка
Один из видов экологической ошибки – это поверхностное допущение, что обо всей разнообразной популяции можно судить по одному статистическому параметру. Так, в Великобритании в 2010 году средняя ожидаемая продолжительность жизни женщин составляла 83 года, а мужчин – всего 79 лет. Общая ожидаемая продолжительность жизни населения, таким образом, составила 81 год. Но утверждение, что любая случайно выбранная женщина будет жить дольше, чем любой случайно выбранный мужчина, сделанное на основании того, что средняя ожидаемая продолжительность жизни у женщин выше, чем у мужчин, и будет типичным примером экологической ошибки. Этот тип ошибки имеет собственное (очень подходящее) название – абстрактное обобщение. Другая распространенная экологическая ошибка – утверждение, что «мы все живем дольше», основанное на поверхностной интерпретации данных об увеличении общей продолжительности жизни. Им часто злоупотребляют ленивые журналисты. Говорить, что все будут жить дольше, чем ожидалось прежде, нельзя. Очевидно, что в лучшем случае это наивные предположения.
Однако экологические ошибки могут быть и менее очевидными. Как ни удивительно, при средней продолжительности жизни в 78,8 года большинство британских мужчин проживет дольше, чем при общей продолжительности жизни населения 81 год. На первый взгляд утверждение кажется противоречивым, но на самом деле это связано со спецификой использования статистических методов для обобщения данных. Небольшое, но значимое количество людей, умирающих молодыми, снижает средний возраст смерти (обычно за общую продолжительность жизни принимают сумму возрастов всех людей на момент смерти каждого, деленную на общее число людей). Как ни странно, эти ранние смерти опускают среднее значение продолжительности жизни намного ниже медианного (возраста, который не переживают столько же людей, сколько и переживают его). Медианный возраст смерти мужчин в Великобритании составляет 82 года, то есть до этих лет доживет как минимум половина из них. В данном случае представленная сводная статистика – средняя продолжительность жизни в 78,8 года – является исключительно недостоверной характеристикой мужской половины британцев.
Гауссова кривая, или кривая нормального распределения, с помощью которой можно описывать самые разные обыденные наборы данных – от роста до показателей IQ, – выглядит как гармоничная симметричная кривая, в которой половина данных лежит на одной стороне среднего значения, а половина – на другой. Это означает, что среднее и медианное – среднее значение распределения данных – значение характеристик, которые подчиняются этому распределению, склонны совпадать. Привыкнув к тому, что эту замечательную кривую можно использовать для описания реальных событий и явлений, многие из нас предполагают, что понятие «среднего» является хорошим маркером «середины» набора данных. Столкновение же с распределениями, где среднее значение не совпадает с медианным, может нас ошарашить. Распределение возраста смерти британских мужчин, показанное на рис. 11, явно далеко от симметрии. Поэтому подобные распределения обычно называют «смещенными» или «асимметричными».
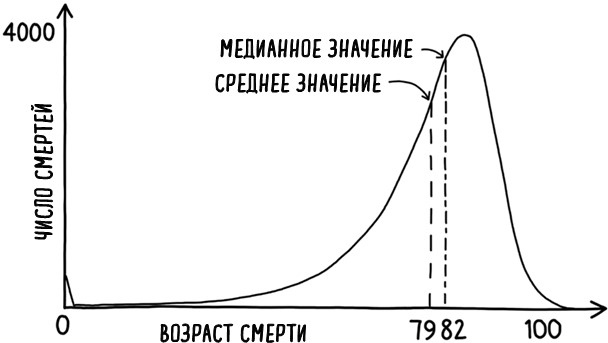
Рис. 11. Возрастная зависимость числа смертей в год у мужчин в Великобритании следует искаженному распределению. Средний возраст смерти составляет чуть менее 79 лет, в то время как медианный возраст – 82 года

