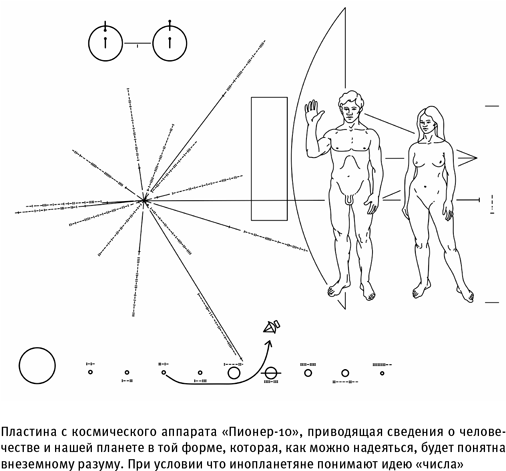
Впрочем, некоторые философы сомневаются, что математика — абсолютно универсальный язык общения, своего рода lingua franca Вселенной
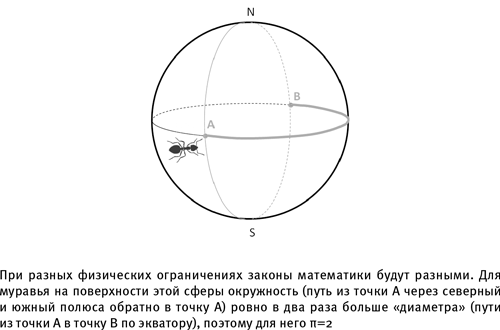
[71]. В частности, наши представления о математике ограничены самими физическими свойствами нашего мира. Мы так привыкли к трехмерному миру, что редко задумываемся о том, насколько будет чужда его математика миру двумерному. Существа размером с муравья, живущие на поверхности маленького шарика, сочтут нашу математику совсем не похожей на свою. Муравей может обойти вокруг своей планетки, воспринимая ее как плоскую поверхность — хотя нам видно, что он на самом деле передвигается по трехмерной сфере. А в мире, где можно ходить только по поверхности сферы (допустим, рыть ходы в ней нельзя), число π не равняется привычным нам 3,14159265… Возьмем точку на экваторе нашей воображаемой муравьиной планеты и окружность, проведенную через ее северный и южный полюса. Наш муравей может обойти свой мир по «окружности» через северный и южный полюса и вернуться в отправную точку. Но «диаметр» этого мира для муравья — путь, перпендикулярный «полярному» маршруту: вдоль экватора к его самой удаленной точке. Этот отрезок, проходящий по экватору, составляет ровно половину окружности планеты, так что в этом случае π=2!
Что касается людей, наш специфический интеллект сформировался в ходе эволюции на равнинах африканских саванн для решения проблем, характерных для африканской саванны
[72]. Мы умеем ловить теннисный мяч, не решая при этом уравнений движения Ньютона, поскольку навыки бросать и ловить развились у нас естественным образом — мы в течение многих поколений бросали копья и ловили животных. Но слепой крот, живущий под землей, может совершенно не понимать, что такое «ловить», и даже не представлять, что это понятие вообще существует, пока какой-нибудь крот-математик, способный к абстрактным озарениям подобно Эйнштейну, не разработает уравнения движения на чисто теоретической основе. Нам трудно воспринимать идеи, лежащие вне нашего чувственного опыта, а чувственный опыт инопланетян, скорее всего, будет непохож на наш.
Помимо ограничений физической среды, развитие математических наук на Земле было обусловлено техническими задачами: усовершенствовать конструкцию храмов (стены должны располагаться под прямым углом к полу), акведуков (арочные пролеты должны обеспечивать устойчивость), катапульт (нужно рассчитать баллистические траектории бросаемых камней), а позже боевых самолетов и атомных бомб, и за всем этим стоят легионы ученых и инженеров. При наших воинственных наклонностях история математических открытий определяется нашим желанием как строить сооружения, так и разрушать их. У мирной инопланетной расы может не возникнуть идея разработки баллистического оружия, а у расы, не имеющей религии, могут так и не развиться технологии строительства величественных храмов. Математические принципы, кажущиеся нам фундаментальными и очевидными, могут иметь гораздо меньше значения для инопланетян, которые достигли своей «разумности» совсем иным путем.
А как насчет элементарной арифметики? Должны ли все разумные инопланетяне, например, уметь считать? Даже если у них нет пальцев или аналогичных органов? Как вообще на Земле эволюция породила математические способности и насколько вероятно, что они будут развиваться похожим эволюционным путем на других планетах?
Эволюция математических способностей
Способность различать понятия «много» и «мало» явно дает животному огромные эволюционные преимущества. Если вы можете определить, где «много» пищи и где «много» хищников, ваша вероятность выжить повышается. Поэтому неудивительно, что едва ли не все животные на всех уровнях развития обладают этой способностью. Однако умение отличить большую кучу еды от маленькой кучки еще не математика. Возможно, вы просто ощущаете более сильный запах от большой кучи или же она занимает бо́льшую область вашего поля зрения, подавая более сильный визуальный сигнал: «иди сюда».
Различие между простой реакцией на сенсорный стимул (пониманием, что с одной стороны запах сильнее, чем с другой) и подлинным умением считать в какой бы то ни было форме (пониманием, что с одной стороны число предметов больше, чем с другой) представляет собой значительный эволюционный шаг. В ходе лабораторных экспериментов ученые искали способы проверить реальные способности животных к счету и отделить умение считать от чувственного восприятия. В итоге на примере нескольких далеких друг от друга видов, от рыб до голубей и обезьян, было показано, что многие животные способны улавливать разницу в числе, а не просто разницу в приблизительном количестве. Хотя до «математики» в нашем понимании здесь еще далеко, эта способность фактически лежит в основе математической компетенции. Вряд ли животное или инопланетное существо сможет развить способность производить сложные математические расчеты, не приобретя сначала базовый навык счета. Наши собственные поразительные возможности в области алгебры, математического анализа и статистики, вероятно, смогли развиться лишь потому, что наши предки умели увидеть разницу между двумя львами и пятью.
Следующая ступень за базовым представлением о количестве — эволюционные преимущества которого вполне очевидны — представление о «числе» как таковом. Это огромный скачок в развитии интеллектуальных способностей, и его гораздо труднее объяснить с эволюционной точки зрения. Если я умею различать «много львов» и «мало львов», так ли уж мне надо точно знать, что передо мной именно три льва? Как таковая, способность различать конкретные числа не так уж распространена среди животных, но и не отсутствует полностью. Эксперименты прежних лет показали, что крыс можно научить дергать за рычаг определенное количество раз, чтобы получить вознаграждение: если дернуть три раза, то получишь лакомство, если четыре — нет. Животные, по-видимому, понимали, что они должны проделывать это определенное число раз, а не руководствоваться простым принципом «больше значит лучше».
Конечно, можно отнестись с некоторой долей скептицизма к поведению крыс в лаборатории: мы уже убедились, что путем ассоциативного научения можно добиться от животного выполнения любого вида заданий, хоть катания на скейтборде. Может быть, это какой-то побочный продукт интенсивного обусловливания, как при обучении цирковых слонов делать вещи, совершенно несвойственные слонам? Хотя интенсивное обусловливание может продемонстрировать, что животные теоретически способны выполнять «интеллектуальные» задачи, этот метод мало что говорит нам о том, действительно ли эти способности развились, чтобы дать им эволюционное преимущество в дикой природе. Напомню, что наша цель — найти универсальные пути к интеллекту, одинаковые для животных нашей планеты и обитателей чужих миров. Нас интересует эволюционная функция интеллекта, а не трюки, которые умеют выполнять животные ради нашего развлечения.




