Рубенс также сообщил о другом открытии: английский физик лорд Рэлей нашел объяснение для низкочастотного конца спектра. Рэлей поставил перед собой такой вопрос: волны какого размера помещаются в таком устройстве, как полостной излучатель? По сути, он заявил, что для длинных волн там меньше места, чем для коротких.
Представьте туго натянутую гитарную струну. Ущипните ее ровно посередине, и зазвучит ее самая низкая — основная — нота. Ущипните ее ближе к концу, и звук окажется другим, потому что вместе с низкой нотой зазвучат и более высокие гармонические тона. Это объясняется тем, что струна может одновременно производить колебания в разных “модах”. В самой низкой моде середина струны колеблется вверх-вниз. В следующей моде струна вибрирует в форме буквы S. Затем — в форме двойной S и так далее. Эти моды называются стоячими волнами.
Электромагнитные волны также создают стоячие волны внутри полостных излучателей. Как мы помним, излучатель имеет цилиндрическую форму. Его концы подобны двум концам гитары. Разные моды помещаются в длину цилиндра, как и моды гитарной струны помещаются в длину инструмента. Однако, по мысли Рэлея, размер полостного излучателя устанавливает ограничения для более длинных волн.
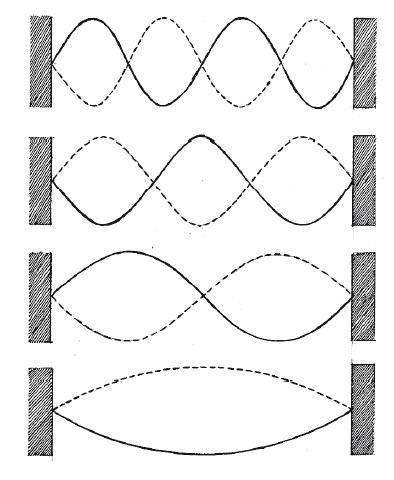
Разные “моды” гитарной струны
Почему? Потому что в полостной излучатель помещается гораздо больше коротковолновых мод, чем длинноволновых. Пусть длина устройства составляет 60 см. В него поместится волна не длиннее 120 см — это первая мода с пиком в середине устройства. Длина следующей составит 60 см — это вторая мода с двумя пиками. Третьей — 40 см, четвертой — 30 см. Таким образом, в диапазоне от 30 до 120 см в излучатель поместятся лишь волны четырех длин. Теперь вычислите, волны скольких длин в диапазоне от 0,5 до 1,5 см поместятся в то же устройство. Ответ: таких длин 79.
Руководствуясь этой логикой, Рэлей пришел к выводу, что полостной излучатель должен испускать меньше длинноволнового излучения, чем коротковолнового. Его аргумент естественным образом вытекал из волновой природы света и, что важнее, позволял сделать математические прогнозы, соответствующие данным для низких частот.
Однако на высоких частотах этот аргумент не работал. Поскольку теоретически количество коротковолновых мод, которые помещаются в полостной излучатель, не ограничено, метод Рэлея предполагал, что даже при низких температурах он должен быть полон ультрафиолетового света и рентгеновских лучей. На самом деле такого излучения почти не было даже при самых высоких температурах.
Что это значит? Если не вдаваться в детали, математические выкладки Планка не соответствовали низкочастотной энергии, наблюдаемой в полостном излучателе, но были верны для высоких частот.
С анализом Рэлея ситуация обстояла наоборот. Его выкладки были верными для низких частот, но значительно завышали показатели для высоких.
Раздосадованный, что у него не получается объяснить эту нестыковку, Планк решился на то, что впоследствии назвал “шагом отчаяния”. “Я готов был пожертвовать любым из своих прошлых убеждений, касающихся физики”, — признался он.
К чему это привело? Посвятив работе пять лет, Планк — вопреки своим надеждам — не вытеснил статистику из термодинамики, а вынужден был расширить ее применение.
Людвиг Больцман использовал статистику, чтобы объяснить, как теплота рассеивается при столкновении атомов и молекул друг с другом. Планк обнаружил, что, лишь применив такие же статистические методы к колеблющимся электронам в стенках полостного резонатора, можно вывести уравнение, точно соответствующее результатам наблюдений. В важнейшей статье 1900 года Планк признал, что ему пришлось прибегнуть к “статистическим представлениям, важность которых для второго закона термодинамики была открыта, прежде всего, г-ном Л. Больцманом”
[20]. Планк пять лет пытался доказать, что Больцман ошибается, но у него ничего не вышло.
Планку пришлось не только применить статистику, но и сделать странное допущение о физическом мире. Представьте, что внутренняя сторона резонатора (замкнутой непрозрачной полости) напоминает пещеру, где на стенах висят колокольчики, каждый из которых имеет свой тон — от низкого звона до высокого “звяканья”. Если бы пещера содрогнулась от мощного землетрясения, все колокольчики зазвенели бы примерно на одной громкости.
Подобным образом в полостном резонаторе есть осцилляторы — обычно в их роли выступают колеблющиеся электроны, которые испускают широкий диапазон электромагнитного излучения, от низкочастотных радиоволн до высокочастотных рентгеновских лучей. При повышении температуры резонатора под действием теплоты осцилляторы начинают дрожать, как колокольчики в пещере. Но здесь проявляется ключевое различие. Планку пришлось допустить, что для излучения высокочастотному осциллятору требуется гораздо больше энергии, чем низкочастотному. Если провести аналогию, то колокольчик высокого тона придется встряхнуть гораздо сильнее, чем колокольчик низкого тона, чтобы он вообще издал звук. Если бы пещера с такими колокольчиками содрогнулась от землетрясения, звон колокольчиков низких и средних тонов поглотил бы звон колокольчиков высоких тонов.
В целом Планк рассудил, что, получая большие порции энергии, осцилляторы испускают высокочастотное излучение. Для низкочастотного излучения нужны гораздо меньшие порции энергии. Представьте два осциллятора. Один может испускать инфракрасный свет, частота которого составляет 300 триллионов циклов в секунду. Второй может испускать синий свет, частота которого составляет 600 триллионов циклов в секунду. Чтобы испустить свет, второму осциллятору понадобится вдвое больше энергии, чем первому. Из этого есть и другое следствие: осцилляторы испускают свет дискретными порциями. В приведенном выше примере это значит, что наименьшая порция синего света содержит вдвое больше энергии, чем наименьшая порция инфракрасного света.
Затем Планк объединил эти идеи с больцмановской статистикой, чтобы объяснить, как горячие тела, такие как полостные резонаторы, печи для обжига и даже звезды, излучают электромагнитную энергию. Чтобы понять, как он это сделал, рассмотрим следующий мысленный эксперимент:
Представьте магазин, где синие конфеты продаются по j долларов за штуку, зеленые — по 3 доллара, а красные — по 1 доллару. В ассортименте также есть крупные, но дешевые бесцветные конфеты, которые продаются всего по 20 центов за штуку. Последних довольно мало, поскольку они занимают очень много места.
Теперь представьте, что у покупателей в среднем есть по 2 доллара на конфеты. У некоторых есть 3 доллара, у немногих — 5. Если через некоторое время подсчитать проданные конфеты, выяснится, что среди них относительно немного синих, зеленых и бесцветных, но много красных. Если бы покупатели были богаче — скажем, если бы большее их число имело по 3 и 5 долларов, — продавалось бы больше зеленых и синих конфет. Суть в том, что обеспеченность клиентов и цвет покупаемых конфет состоят не в прямой, а в статистической зависимости.



