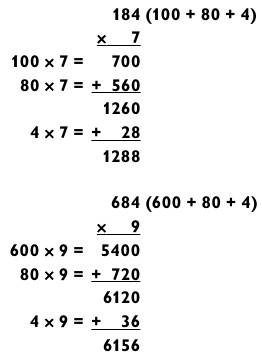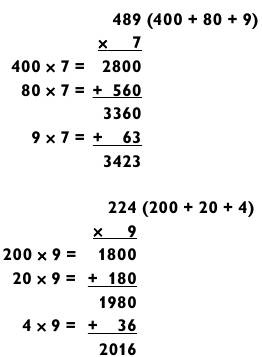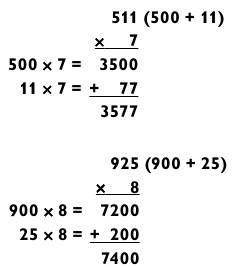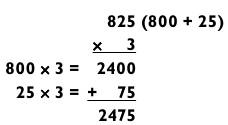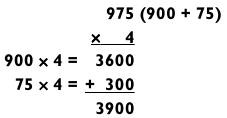Поднимемся на новый уровень сложности и попробуем решить пару примеров, которые потребуют от нас удержания чисел в уме.
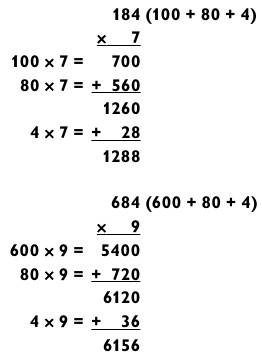
В следующих двух примерах вам нужно держать числа в уме на последнем этапе решения, а не в его начале.
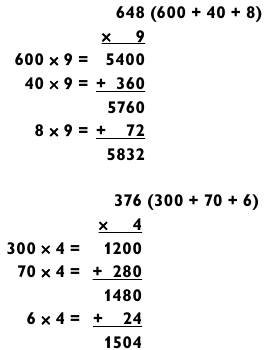
Первое действие для каждой задачи легко выполнить в уме. Сложности возникают при необходимости удерживать в памяти предварительный ответ, параллельно вычисляя итоговый. В первой задаче легко сложить 5400 + 360 = 5760. Но вы будете вынуждены твердить «5760» самому себе, пока умножаете 8 х 9 = 72. Затем надо сложить 5760 и 72. Иногда на этой стадии я начинаю проговаривать ответ вслух еще до ее завершения. Я знаю, что нужно будет держать числа в уме, когда я буду складывать 60 + 72, но я также знаю, что 5700 станет 5800.
Я говорю: «Пять тысяч восемьсот…», затем приостанавливаюсь для сложения 60 + 72 = 132. Поскольку я уже держу числа в уме, я произношу только последние две цифры: «… тридцать два!» А вот и ответ: 5832.
Две следующие задачи потребуют от вас держать в уме два числа, так что их решение может занять больше времени. Но, потренировавшись, вы станете делать это быстрее.
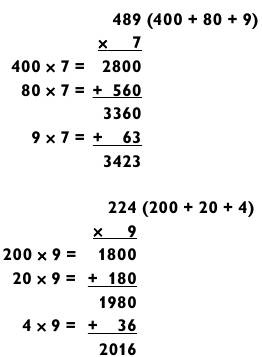
Когда вы впервые принимаетесь за решение таких примеров, повторяйте ответы для каждого действия вслух, параллельно вычисляя остальное. В первой задаче, например, начните с «две тысячи восемьсот плюс пятьсот шестьдесят», проговорив пару раз все это вслух и тем самым закрепив два числа в памяти, пока складываете их. Повторите ответ «три тысячи триста шестьдесят» несколько раз, пока умножаете 9 х 7 = 63. После проговаривайте «три тысячи триста шестьдесят плюс шестьдесят три» вслух до тех пор, пока не вычислите итоговый ответ 3423. Если вы достаточно быстро соображаете, чтобы распознать, что сложение 60 + 63 потребует переноса 1 в старший разряд, то вы в состоянии назвать итоговый ответ на долю секунды быстрее, чем сами это осознаете: «три тысячи четыреста и… двадцать три!»
Завершим раздел с задачами на умножение типа «3 на 1» рядом особых примеров, которые можно мгновенно решить, так как они требуют лишь одного действия на сложение вместо двух.
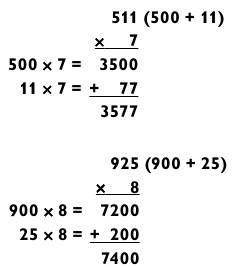
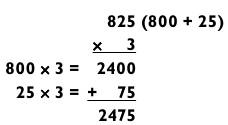
В общем, если результат умножения последних двух цифр первого числа на его множитель известен вам и без подсчетов (например, вы знаете, что 25 х 8 = 200), то вы сможете получить итоговый ответ намного быстрее. Например, если вы и так знаете, что 75 х 4 = 300, то легко вычислите 975 х 4.
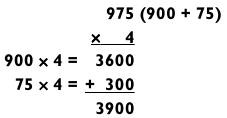
Чтобы закрепить только что усвоенный материал, решите следующие задачи на умножение типа «3 на 1» в уме, а затем проверьте себя по ответам в конце книги. Исходя из собственного опыта, могу сказать, что устные вычисления сродни катанию на велосипеде или печатанию. Это может казаться невозможным поначалу, но как только вы все освоите, то уже никогда этого не забудете.

ВОЗВЕДЕНИЕ В КВАДРАТ ДВУЗНАЧНЫХ ЧИСЕЛ
Возводить в уме числа в квадрат (умножать число само на себя) — одно из наиболее легких, но в то же время и наиболее впечатляющих ловкачеств из арсенала устных вычислений. Я до сих пор помню, как открыл этот прием для себя. Мне было тринадцать. Я ехал в автобусе навестить отца на работе в центр Кливленда. Я уже проделывал этот путь неоднократно, поэтому мысли начали блуждать. Не помню почему, но я стал думать о числах, которые в сумме дают 20. И задался вопросом: насколько большим может быть произведение этих чисел?
Я начал с середины, 10 х 10 (или 102) равняется 100. Затем я умножил 9 х 11 = 99; 8 х 12 = 96; 7 х 13 = 91; 6 х 14 = 84; 5 х 15 = 75; 4 х 16 = 64 и т. д. и обратил внимание на то, что результат каждый раз уменьшается. И разность между ним и 100 составляет 1, 4, 9, 16, 25, 36… или 12, 22, 32, 42, 52, 62… (смотри таблицу ниже).
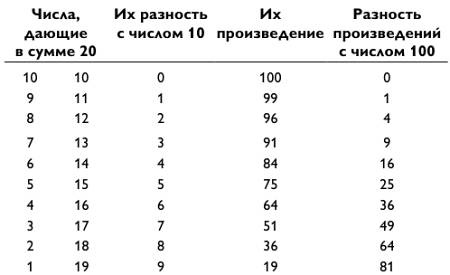
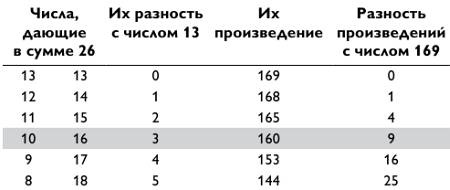
Мое открытие показалось мне удивительным. Затем я опробовал числа, дающие в сумме 26, и получил похожие результаты. Первым делом я вычислил 132 = 169, затем 12 х 14 = 168; 11 х 15 = 165; 10 х 16 = 160; 9 х 17 = 153 и т. д. Как и прежде, разность этих произведений и числа 169 равнялась 12, 22, 32, 42…
(смотрите таблицу ниже).
На самом деле существует простое алгебраическое объяснение данного феномена (смотрите раздел «Почему эти приемы работают» в конце главы). Но в то время я не разбирался в алгебре настолько хорошо, чтобы доказать постоянство появления такой последовательности, но все-таки провел достаточное количество экспериментов с подобными примерами, чтобы убедиться в ее наличии.
Затем я осознал, что данная последовательность может облегчить операцию возведения чисел в квадрат. Предположим, я хочу возвести в квадрат число 13. Почему бы, вместо того чтобы умножать 13 х 13, не получить приближенный ответ, используя два числа, которые легче перемножить и которые в сумме дают тоже 26? Я выбрал 10 х 16 = 160. Чтобы получить итоговый ответ, я просто прибавил 32 = 9 (так как 10 и 16 дают разность 3 с числом 13) к числу 160. Таким образом, 132 = 160 + 9 = 169. Все четко!