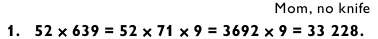
Запомнив число 33 228 с помощью мнемоники Mom, no knife, далее переключаюсь на вторую задачу типа «3 на 2».
2. 27 х 196 = 27 х (200 — 4) = 5400 — 108 = 5292.
И прибавляю этот результат к числу, которое хранится в памяти.
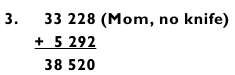
Получаем новую сумму и сохраняем ее в уме как:
Movie lines (38 миллионов, 520 тысяч)
Запомнив этот мнемонический код, решаем задачу «2 на 2».
4. 52 х 27 = 52 х 9 х 3 = 1 404.
На данном этапе уже можно дать частичный ответ. Поскольку задача «2 на 2» — это перемножение миллионов, то 1 404 означает 1 миллиард 404 миллиона. Так как 404 миллиона не подразумевают переноса единицы в разряд миллиардов, то можно спокойно произнести: «Один миллиард…».
5. 404 + Movie (38) = 442.
Теперь прибавляем 404 к movie (38), получается 442. В этот момент можно сказать «…442 миллиона…». Это можно сделать потому, что на 442 не будет переноса единицы. Чтобы удостовериться в этом, надо посмотреть наперед на задачу типа «3 на 3». Если ее ответ говорит о переносе единицы, то надо сказать «443 миллиона». Но так как результат задачи «3 на 3» (639 х 196) не превысит 500 000 (что показывает грубая оценка 600 х 200 = 120 000), этого не произойдет.
6. 639 х 196 = 639 х 7 х 7 х 4 = 4 473 х 7 х 4 = 31 311 х 4 = 125 244.
Все еще удерживая в голове слово lines, решаем задачу «3 на 3» с помощью метода разложения и получаем 125 244.
Чтобы запомнить число 244, переводим его в слово nearer.
Итоговое действие представляет собой простое сложение:
7. 125 244 + Lines (520 000) = 645 244.
Это позволяет произнести оставшуюся часть ответа: «…645 244».
Так как один рисунок стоит тысячи слов, вот схема всех выполненных вычислений в данном примере.
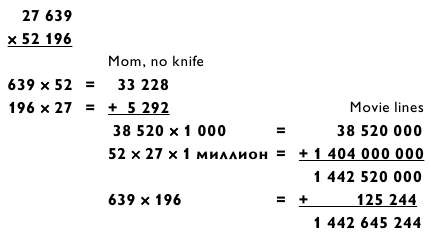
Здесь необходимо сделать небольшое замечание о моем предположении, что при решении задачи типа «5 на 5» у вас есть возможность записать ее условие на доске или бумаге.
Если такой возможности нет, то вам придется задать мнемонический код для всех четырех чисел (два исходных числа и два промежуточных результата). Например, условие предыдущей задачи можно запомнить в виде слов:
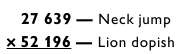
Потом надо умножить lion х jump (52 х 639), dopish х neck (196 х 27), lion х neck (52 х 27) и, наконец, dopish х jump (196 х 639). Очевидно, эти действия несколько замедлят процесс вычислений, но если вы хотите решать задачи не глядя на их условия, то после тренировок будете в состоянии это делать.
Закончим главу еще одним примером «5 на 5».

Последовательность действий в этом примере такая же, как и при решении предыдущего. Начинаем с самой сложной задачи типа «3 на 2» и сохраняем ответ в виде мнемонического кода.
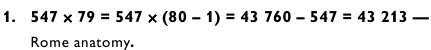
Затем решаем вторую задачу типа «3 на 2».
2. 838 х 45 = 838 х 5 х 9 = 4190 х 9 = 37 710.
Суммируем полученное и вверяем итог своей памяти.

4. 79 х 45 = 79 х 9 х 5 = 711 х 5 = 3 555.
Результат задачи «2 на 2» дает первую цифру окончательного ответа, которую с уверенностью можно произнести вслух: «Три миллиарда…».
5. 555 + Face (80) = 635.
Миллионы в ответе содержат перенос единицы, то есть число 635 надо заменить на 636, потому что к числу Panama (923) достаточно прибавить 77 000, чтобы превысить 100 000 и вызвать перенос единицы. А результат задачи «3 на 3» (838 х 547) с легкостью превысит это значение. Поэтому следует сказать: «…636 миллионов…».
Задача «3 на 3» была посчитана с использованием метода сложения.
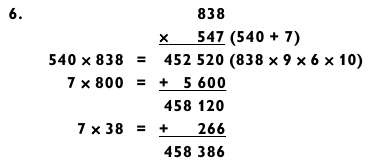
На следующем этапе прибавляем этот результат к числу Panama (923 000).
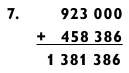
Так как перенос числа 1 мы уже использовали при получении 636 миллионов, нам осталось лишь проговорить тысячи: «…381 тысяча…386» и насладиться аплодисментами!
Решение данной задачи схематически можно представить следующим образом:


Глава 9
Искусство математической магии
Я всегда получал удовольствие от игры с цифрами. Я нахожу арифметику такой же занимательной, как и магию. Но понимание магических секретов арифметики требует знаний алгебры. Конечно, есть и другие причины для ее изучения. Назову лишь несколько: сдача экзаменов, моделирование проблем из реального мира, программирование и возможность понимания высшей математики. Но интерес к алгебре у меня вызвало в первую очередь желание понять некоторые математические трюки. Их я вам сейчас и представлю!

