Упражнение 33. Конфеты (2)
Какова вероятность вытащить за один раз красную или желтую конфету? Какова вероятность вытащить желтую или зеленую? Запишите ответы на листке бумаги.

Вероятность вытащить красную или желтую конфету: 0,5 + 0,4 = 0,9.
Вероятность вытащить желтую или зеленую конфету: 0,4 + 0,1 = 0,5.
Важно понимать: наше «или» означает необходимость сложить вероятности отдельных событий. Многие этого не осознают, пока как следует не разберутся, из чего я делаю вывод, что такая концепция человеку интуитивно не очевидна. И даже после объяснения многие этот принцип понимают не до конца. Как писал Кэмпбелл, люди не запоминают правил расчета вероятности, даже когда применяют их для решения задач. Поэтому большинству из нас нужно всякий раз выводить эти правила заново.
Давайте попрактикуемся: построим дерево вероятностей и рассчитаем вероятности.
Упражнение 34. Лиса в курятнике
В курятнике 50 кур: десять рыжих, пять черных, 15 коричневых, 20 белых. Если лиса проберется в курятник и наугад схватит одну из куриц, какова вероятность того, что ей попадется рыжая или коричневая курица? На листе бумаги постройте дерево вероятностей, отметьте на нем кур всех типов, посчитайте вероятность того, что лиса схватит курицу каждого из цветов по отдельности, а затем ответьте на вопрос задачи.

На рис. 13.3 показано дерево вероятностей.
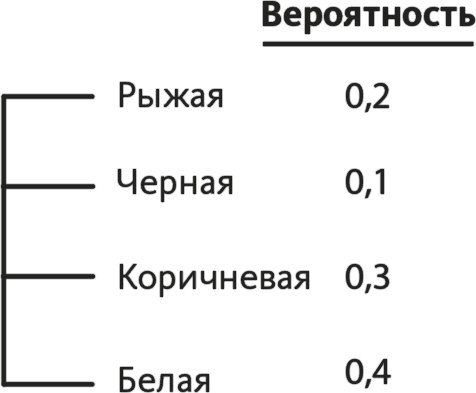
Рис. 13.3
Вероятность поймать рыжую курицу составляет 0,2, вероятность поймать коричневую – 0,3. Поэтому вероятность поймать рыжую или коричневую курицу составляет 0,2 + 0,3 = 0,5.
Вероятность взаимосвязанных событий
Как рассчитывается вероятность взаимосвязанных событий? Перемножением вероятностей всех этих событий. Сейчас я объясню, почему это так.
Какова вероятность, что при подбрасывании монеты два раза подряд выпадет орел?
На рис. 13.4 представлено дерево вероятностей, иллюстрирующее все возможные последовательности событий. Вероятность, что при первом броске выпадет орел, равна 0,5. Если выпадает решка, эксперимент заканчивается, так как нам нужно, чтобы орел выпал два раза подряд. Поэтому второй раз мы бросаем монету, только если в первый раз выпал орел. То есть второй бросок зависит от результата первого: между этими событиями существует взаимосвязь. Если в первый раз выпадает орел, то какова вероятность, что и во второй раз выпадет орел? По-прежнему 0,5. То есть мы получаем 50 %-ную вероятность от 50 %-ной вероятности (0,5 умножить на 0,5), что два раза подряд выпадет орел. Вероятность наступления этих двух последовательных событий равна 0,25.

Рис. 13.4
Давайте рассчитаем вероятность взаимосвязанных событий на примере задачи с конфетами. Какова вероятность того, что мы вытащим вначале красную конфету (и вернем ее в банку), а сразу за ней зеленую? Цепочка событий представлена на рис. 13.5. Вероятность вытащить красную конфету равна 0,5; вероятность вытащить зеленую конфету, без привязки к красной, – 0,1. Поэтому вероятность вытащить красную, а потом зеленую конфету равна 0,5 × 0,1 = 0,05.
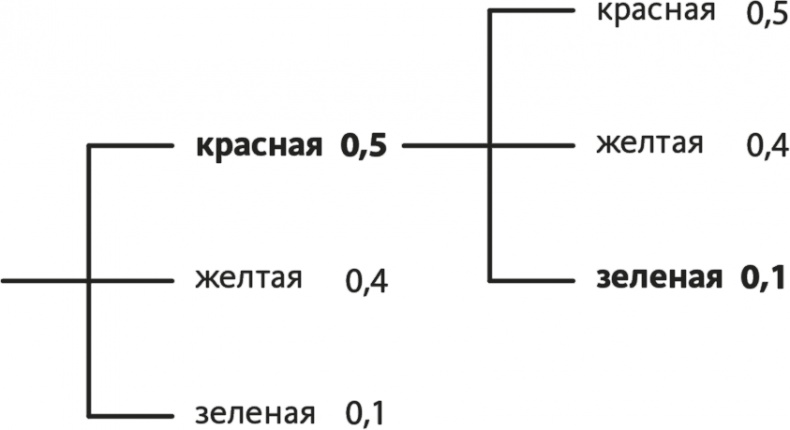
Рис. 13.5
Упражнение 35. Медвежатник (2)
Давайте вернемся к нашей задаче о взломщике сейфов. Вам нужно пройти через пять дверей, в каждой из которых кодовый замок. Вы вор, и уже девять раз из десяти вам удавалось верно подобрать код к такому замку; только на десятый раз вы не справились. Какова вероятность того, что вы сможете открыть все пять дверей?
Здесь требуется расчет вероятности взаимосвязанных событий, потому что вы перейдете ко второй двери, только если откроете первую, а к третьей – только если откроете вторую, и так далее.
Какова вероятность (В1) того, что вы сможете пройти через первую дверь? Мы можем рассчитать вероятность, исходя из ваших прежних результатов: девять из десяти. Какую долю от 10 составляет 9? 90 %, то есть В1 = 0,9.
Какова вероятность открыть и первую, и вторую двери? Возможность открыть вторую дверь зависит от того, открыли ли вы первую. Таким образом, мы должны умножить вероятность открыть первую дверь (0,9) на вероятность открыть вторую дверь. Думаете, вероятность открыть вторую дверь тоже 0,9? Нет, ответ неверный. Это была вероятность открыть первую дверь, которую мы рассчитали, исходя из того, что в прошлом вы смогли открыть 9 дверей из 10. Но после того как вы открыли первую из этих пяти дверей, ваш результат изменился: в совокупности вы успешно открыли уже 10 дверей из 11. То есть вероятность открыть вторую дверь составляет 10 / 11 = 0,91. Тогда вероятность открыть и первую, и вторую двери равна 0,9 × 0,91 = 0,82. Пока все понятно? Если нет, вернитесь к началу этого объяснения и перечитайте.
Рассчитайте вероятность того, что вы сможете открыть пятую дверь и украсть бриллиант. Запишите расчеты и ответ.

Предлагаю вам решение задачи:
В1 = 9 / 10 = 0,9;
В2 = 0,9 × (10 / 11) = 0,82;
В3 = 0,82 × (11 / 12) = 0,75;
В4 = 0,75 × (12 / 13) = 0,69;
В5 = 0,69 × (12 / 14) = 0,64.
Сравните 0,64 с со сделанным вами выше предположением о том, какова вероятность, что вы сможете украсть бриллиант. Насколько близка ваша оценка к расчету? Большинство склонны считать, что вероятность открыть все пять дверей и добраться до бриллианта довольно высока. Если вы ошиблись в оценке вероятности в задаче «Медвежатник (1)», не огорчайтесь: как я уже говорил, вероятность кажется большинству из нас одной из наиболее сложных для понимания и применения концепций. Ее совершенно невозможно понять интуитивно. Поэтому важно разобраться, чем отличаются взаимоисключающие и взаимосвязанные события и их вероятности, и как можно больше практиковаться в расчетах вероятности. Только так оценка вероятности станет понятной и привычной.








