Или мы захотели узнать, насколько сильна корреляция между тем, где человек живет, и его умением водить машину. Мера, о которой мы говорили до сих пор, применяется для неквантованных
[116] данных, таких как цены на акции, а не дискретных, таких как местонахождение или киножанр. Если у нас всего две переменные, каждая из которых принимает только два значения, лучше взять упрощенный вариант коэффициента корреляции Пирсона – так называемый фи-коэффициент
[117].
Например, можно проверить соотношение между местом, где люди живут, и их умением водить машину. Местом жительства может быть либо город, либо пригород / сельская местность, а факт вождения может либо иметь место (да), либо нет. Как и ранее, проверяем, как эти условия варьируются. Здесь вариация означает частоту, с которой они наблюдаются совместно (а не то, как значения увеличиваются или уменьшаются).
В табл. 3.1 показано, какой вид могут принимать данные. Фи-коэффициент для них составляет 0,81. Мы изначально смотрим, сосредоточено ли большинство измерений вдоль диагональной линии на таблице. Если значения в основном находятся в группах вождение/не-город и не-вождение/город, можно говорить о положительной корреляции.
Если аккумулируются вдоль другой диагонали, корреляция имеет такую же силу, но другой знак.
Таблица 3.1. Различные комбинации местонахождения и вождения

Однако на основе этих измерений не каждая сильная корреляция будет иметь высокое значение. Применение коэффициента Пирсона предполагает, что это отношение линейно, а значит, если одна переменная (например, рост), увеличивается, другая (например, возраст) также увеличивается, причем с одинаковым темпом. Это не всегда справедливо, поскольку могут встречаться и более сложные, нелинейные отношения. К примеру, если из-за нехватки кофе человек становится вялым (и не способен показать хорошие результаты на экзамене), а избыток кофе его возбуждает (и тоже плохо влияет на результаты), то график, выстроенный на основе некоторых данных, может иметь вид, как на рис. 3.4. Здесь видно повышение балла в диапазоне от 0 до 5 чашек кофе, потом еще одно медленное падение. Хотя корреляция Пирсона для этого примера нулевая, данные показывают четкий паттерн.
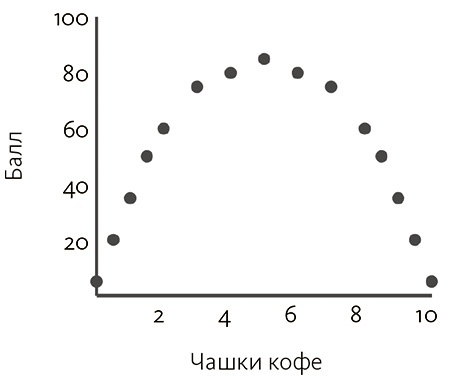
Рис. 3.4. Нелинейное отношение (r = 0,000)
Подобный тип отношений показывает неоднозначные результаты при многих методах причинных умозаключений. В последующих главах мы вернемся к этому. Его важно иметь в виду, поскольку он встречается в таких прикладных науках, как биомедицина (например, и недостаток, и передозировка витаминов могут иметь последствия для здоровья) и финансы (например, кривая Лаффера, которая показывает зависимость между доходами государства и динамикой налоговых ставок).
Аналогично, если вес детей всегда увеличивается с возрастом, но экспоненциально (дети растут, и их вес растет все сильнее), корреляция Пирсона будет ниже ожидаемой, так как она работает в линейных зависимостях. Это одна из опасностей, подстерегающая тех, кто бросает данные в «черный ящик» и просто принимает любые полученные результаты, не проводя дальнейших исследований. Поступив так, когда корреляция недооценивается или даже кажется равной нулю, мы упускаем потенциально интересные зависимости.
Это одна из причин, почему нельзя интерпретировать нулевую корреляцию (пирсоновскую или любую другую) как вообще незначимую (существуют и другие причины, например ошибки в измерениях или первичные данные, искажающие результаты). Еще одна важная причина заключается в том, что данные могут не быть репрезентативными с точки зрения исходного распределения. Если бы нам разрешили взглянуть на статистику смертей от гриппа, но предоставили только данные о количестве больных, поступивших в лечебные учреждения, и вызовов скорой помощи, мы наблюдали бы гораздо более высокий процент летальных исходов, чем в масштабах всего населения. Это происходит потому, что люди оказываются в стационаре, как правило, с более тяжелыми случаями или дополнительными заболеваниями (и с высокими шансами смерти от гриппа). Итак, мы снова сравниваем не все исходы, а только статистику для больных или обратившихся к врачам на фоне симптоматики гриппа.
Чтобы проиллюстрировать эту проблему в ограниченном диапазоне, возьмем, к примеру, две переменные: общий экзаменационный балл и часы, потраченные на подготовку. Однако вместо данных по всему спектру оценок за экзамен мы имеем только сведения о лицах, получивших общий балл за письменный и устный тест по математике выше 1400. На рис. 3.5 эта область показана серым цветом.
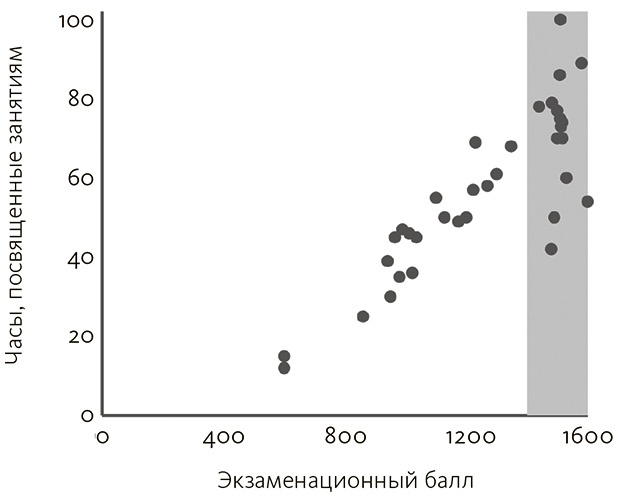
Рис. 3.5. Закрашенная область представляет ограниченный диапазон данных
Согласно этим гипотетическим показателям, студенты с высокими баллами представляют собой комбинацию как лиц с природной одаренностью (которые преуспевают, особо не утруждаясь), так и тех, кто получил лучшие оценки за счет интенсивных занятий. Если воспользоваться только данными из закрашенной области, мы не обнаружим никакой корреляции между переменными; но если применить информацию по всему спектру экзаменационных показателей, созависимость будет сильной (корреляция Пирсона оценки и упорных занятий для закрашенной области равна 0, а для всего набора данных – 0,85).
Оборотная сторона медали – это корреляции, которые мы порой находим между несвязанными переменными, опираясь только на следствия (то есть принимая во внимание только случаи, когда это следствие имеет место). К примеру, получение высокого экзаменационного балла и участие во множестве факультативных мероприятий обеспечивают прием в престижный университет. Значит, данные, взятые только в вузах, покажут корреляцию между высоким баллом и многочисленными факультативами, так как здесь эти показатели чаще всего в наличии.
Подобная тенденция отбора данных довольно типична. Возьмем, к примеру, сайты, опрашивающие посетителей насчет их политических взглядов. В интернете не получится отобрать участников опроса случайно в масштабах всего населения, а данные источников с сильным политическим уклоном искажены еще сильнее. Если посетители конкретной страницы активно поддерживают действующего президента, то результаты по ним, возможно, покажут, что рейтинг главы государства растет каждый раз, когда он произносит важную речь. Однако это показывает лишь то, что есть корреляция одобрения президента и произнесения им речей перед сторонниками (поскольку на вопросы отвечают представители всего населения). Мы рассмотрим и эту, и другие формы трендов (например, смещение по выживаемости) в главе 7 и увидим, как они влияют на результаты анализа экспериментальных данных.





