Один из самых знаменитых в истории примеров применения методов Милля – когда Джон Сноу обнаружил, что именно спровоцировало вспышку холеры 1854 года в Лондоне
[194]. Он не копировал методы Милля, однако используемый им подход строился по тому же принципу.
Тогда никто не знал, каким путем распространяется болезнь, но карта города (с нанесенными очагами инфекции) дала возможность увидеть резкие отличия между районами. Передавался ли возбудитель от одного человека к другому? Или болезнь вызвало что-то по соседству? А может, у людей, проживающих в зараженных районах, имелось нечто общее?
Сноу обнаружил, что самая высокая смертность отмечалась не просто в конкретном географическом районе, а возле водяной колонки на Брод-стрит:
В домах, расположенных ближе к колонке на другой улице, умерли всего 10 человек. В пяти случаях из этих 10 родственники больных сообщили, что они всегда ходили к колонке на Брод-стрит, потому что предпочитали воду из нее другим колонкам, даже если те располагались ближе. В трех других случаях это были дети, которые шли в школу мимо колонки на Брод-стрит
[195].
Увидев, что умершие в основном пользовались этой колонкой, Сноу рассмотрел, видимо, не соответствующие этой тенденции случаи, когда люди не жили по соседству, и выяснил, что они тоже брали воду на Брод-стрит. Это и есть в точности метод согласованности Милля, где выясняется, что общего у всех случаев наступления следствия (например, заболевание холерой). Сноу также применял метод дифференциации, когда писал, что «в этой части Лондона не отмечалось никаких особых вспышек или заболеваемости холерой, кроме как среди людей, имеющих обыкновение пить воду из вышеупомянутой колонки»
[196]. Иными словами, доказал, что заболеваемость возросла в группе лиц, пользовавшихся колонкой, и только в этой группе.
Комплекс причин
Единственная проблема с методами Милля – ситуация, когда причина обусловливает, с той или иной долей вероятности, зависимость следствия от иных факторов. К примеру, два лекарственных препарата сами по себе могут не влиять на содержание глюкозы в крови, однако, взаимодействуя при одновременном приеме, способны существенно повысить ее показатель. Один из вариантов преодолеть эту трудность – не концентрироваться на парных зависимостях между отдельно взятыми причинами и следствиями, но рассматривать комплекс условий, вызывающих следствие. Так, одной из причин дорожного происшествия может быть нетрезвое вождение в комбинации с близко проезжающими машинами, другой – плохая видимость на обледеневшей дороге и неосторожное вождение, третьей – нарушение скоростного режима и отправка электронных сообщений за рулем.
Подобные ситуации часто возникают в эпидемиологии, где принято считать, что причины всегда взаимосвязаны, и такие факторы, как длительная подверженность окружающим условиям, образ жизни, острые кратковременные воздействия (например, инфекционные заболевания) и так далее, комбинированно влияют на здоровье. Взяв за основу подобные рассуждения, эпидемиолог Кеннет Ротман
[197] ввел идею изображения таких комплексов причин в виде секторных диаграмм
[198].
Секторная диаграмма причинно-следственных связей – группа факторов, достаточных для возникновения следствия, которая содержит все необходимые для этого компоненты. На рис. 5.2 изображены такие диаграммы для всех трех примеров с вождением.
.
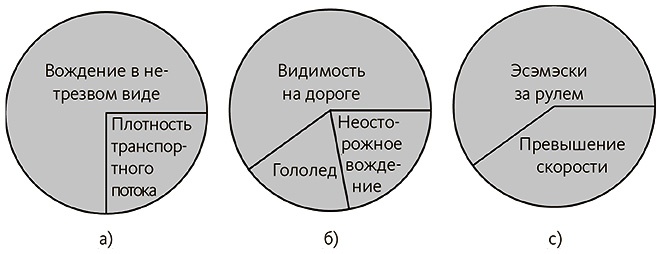
Рис. 5.2. Три причинных комплекса дорожных происшествий
В этом примере каждая диаграмма – достаточное условие для наступления следствия, поэтому ДТП произойдет в каждом случае присутствия этих факторов. Но каждый из них по отдельности не необходимый, поскольку лишь множество условий вызывают следствие. Соблюдение требования, что причина всегда производит следствие (по утверждениям Милля и Юма), в то время как могут существовать необходимые условия для проявления следствия, которых нет в наличии; или что причина есть необходимое условие каждого случая проявления следствия, когда может быть множество возможных его причин, – это исключительно жесткие рамки. В реальности разнообразные следствия могут проявляться множеством различных путей, для чего часто требуется целый набор факторов.
Таким образом, согласно одной из концепций, причина есть компонент группы факторов, которые вместе оказываются достаточным условием возникновения следствия. Правда, такая группа может не быть необходимой, поскольку их способно оказаться множество. Этот подход разделяет Джон Маки
[199], который описывает причины как INUS (недостаточные, но необходимые компоненты не-необходимых, но достаточных условий)
[200]. В примере с секторными диаграммами каждый «кусочек пирога» сам по себе недостаточен (поскольку, чтобы вызвать следствие, нужны другие кусочки), но необходим (потому что, если какой-нибудь кусочек будет упущен, следствие не возникнет). С другой стороны, любая диаграмма (или «пирог») сама по себе не необходима, поскольку таких пирогов может быть много и каждый окажется достаточным условием следствия.
Итак, вместо того чтобы пытаться выделить такие факторы, как экономика, рекламные кампании конкурентов или рейтинги общественной поддержки, в качестве единственной причины результатов выборов, мы отобразим все сопутствующие факторы и, возможно, попробуем выяснить их относительную значимость.
Но не все причины становятся необходимыми INUS-условиями. К примеру, причинно-следственная связь может не иметь характер детерминизма, так что, даже если бы мы владели всей возможной информацией и наблюдали все необходимые условия, следствие не всегда возникало бы. Один из примеров индетерминизма – радиоактивный распад, где никогда нельзя знать наверняка, будет ли иметь место распад частицы в конкретный момент времени: нам известна только вероятность события. INUS-условие распада – вещь невозможная, поскольку достаточных условий здесь не существует. Точно так же могут наблюдаться INUS-условия, не оказывающиеся причинами, если, как в примере с пиццей и водой, у нас нет корректного набора переменных. Точность и полнота логических выводов всегда зависят от полноты данных.



