Если у нас есть представление о видах вероятных структур, можно сгенерировать вероятностное распределение на основе набора графов и с его помощью сориентироваться по поводу возможных структур для исследования
[250].
Как вариант, вместо изучения устрашающе огромного набора потенциальных графов можно использовать зависимости между переменными для построения графа. Методы на основе ограничений предназначены именно для этого: для тестирования по критерию независимости и применения результатов, чтобы добавлять, удалять или ориентировать ребра графа.
Одни методы предусматривают добавление переменных по очереди, а другие начинают со связывания всех переменных друг с другом и удаления ребер по одному
[251].
Возьмем следующий граф, где три переменные соединены всеми возможными путями.
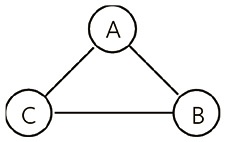
Если мы обнаружим, что А и В независимы при условии С, сможем удалить ребро между ними и продолжить поиск иных взаимосвязей, позволяющих так же снимать ориентировочные ребра. Порядок тестирования, однако, имеет значение, поэтому ошибка на первых шагах может привести к заблуждениям в последующих. Имея реальные данные, вряд ли можно обнаружить точную независимость, однако придется решить, в какой точке принять или отвергнуть гипотезу. То есть, если вероятность А при условии В в точности равна вероятности А, имеет место их независимость. Однако можно обнаружить, что вероятность А при условии В и С очень близка к вероятности только при условии С, но не равна ей.
На практике необходимо выбирать статистический порог, чтобы принять заключение об условной независимости на основе таких тестов. И если необходимо провести большое количество тестов, мы столкнемся со множеством проблем по проверке разнообразных гипотез, о которых говорилось ранее (вспомните эксперимент с дохлым лососем)
[252].
Измерение причинности
Один из подходов к причинному осмыслению – попытка найти модель, удовлетворяющую данным или объясняющую их. Но сделать это вычислительными методами крайне сложно, и в ряде случаев мы просто хотим узнать о взаимосвязях в некоем наборе уже измеренных переменных. То есть, возможно, нам нужно всего лишь выяснить причины рабочей производительности, а не выстроить полную модель, включающую все измеренные переменные. Рандомизированные испытания занимаются именно этими вопросами (каково действие конкретного лекарства на уровень смертности?), однако эксперименты можно проводить не во всех случаях, и им свойственны собственные ограничения (см. главу 7).
Еще один вид причинно-следственных рассуждений связан с квантификацией силы индивидуальных каузальных зависимостей. Если отпуск – причина производительности, а не наоборот, то сила отпуска как причины производительности должна быть выше, а обратной посылки – ниже. Эти корреляции симметричны, но мера каузальной значимости должна учитывать асимметрию таких отношений. Кроме того, она должна в некотором смысле быть пропорциональна информативности причины относительно следствия, а также ее полезности как цели вмешательства для получения следствия. Если отпуск случайно спровоцировал производительность, при этом многочасовая работа всегда ее повышает, тогда отработанные часы имеют больше каузальной силы, чем дни отдыха. Аналогично если принуждать людей брать отпуск – эффективная стратегия повышения производительности, а заставлять работать по многу часов – нет, перерыв в работе окажется более значимой причиной производительности.
Если, однако, отпуск ведет к производительности только потому, что снижает текучку персонала, а более опытные сотрудники демонстрируют более высокую производительность труда, желательно убедиться, что весомость опыта для производительности выше, чем значимость отпуска. То есть требуется найти самые непосредственные причины (на рассмотренных нами графах это родительские переменные, а не отдаленные потомки).
Но, если мы в силах оценить причины производительности совершенно независимо от причин любой другой переменной, можно выполнить меньше тестов, причем реально проводить их параллельно друг другу (что повышает эффективность компьютерных программ для расчета этих переменных). Также это означает, что вместо применения аппроксимации
[253] (например, исследования подгруппы графов, а не всех возможных), когда многократный прогон программы каждый раз дает разные результаты, расчеты будут достаточно просты, чтобы использовать точные методы.
С другой стороны, есть ограничение: без структуры, показывающей связи между всеми переменными, нельзя брать полученные результаты непосредственно для прогнозирования. Скажем, мы обнаруживаем, что партийная поддержка – это причина, по которой сенаторы голосуют за законопроекты, и поддержка избирателей тоже может быть причиной. Но это ничего не говорит о взаимодействии между этими двумя видами поддержки, а также о том, будет ли результат сильнее, чем просто сумма двух причин. Одно из решений – найти более сложные взаимосвязи. Вместо того чтобы использовать любые измеренные переменные, можно выстроить конъюнкцию («законопроект поддерживают и партии, и избиратели»), выяснить, как долго некий фактор должен быть истинным (день, месяц, год и т. д.), и найти последовательности событий (будут ли результаты одинаковыми, если начать прием первого лекарства перед вторым?).
Не вдаваясь в детали, скажем, что существуют методы как для представления, так и для тестирования такого рода сложных взаимосвязей
[254].
Значимость вероятностной причинной связи
Одна из возможных мер каузальной значимости – условная вероятность следствия при условии причины. Проще говоря, мы можем посмотреть, насколько отпуск повышает вероятность высокой производительности труда. Однако, как мы увидели в предыдущей главе, многие непричины также усиливают возможность других событий. Если отработанные часы и отпуск имеют общую причину, то они, по всей видимости, умножают вероятность друг друга.
Есть масса мер силы причинно-следственных связей
[255], однако главное – каким-то образом включить сюда другую информацию и учесть общие причины. Так, допустим, мы знаем, что и отпуск, и сверхурочные увеличивают производительность труда, но, если присутствуют только сверхурочные, одно только знание об отпуске производительность не повысит.



