Чтобы обойтись без вандализма, кто-то предлагает поставить коробку перед слайдопроектором. Тень, измеренная на экране, поможет найти правильный результат при условии, что диагональ коробки расположена строго вертикально и вы помните теорему Фалеса и свойства треугольников.
Менеджер более высокого уровня, раздраженный поворотом событий, без сомнения, предложит кому-нибудь позвонить. Привычка отдавать поручения помогает (в случаях, когда на семинар приходят члены исполнительного комитета, эта идея, как правило, оказывается первой).
Легкие изменения в задании оказывают влияние на очередность поступающих ответов. Если в вашем распоряжении кирпич, стеклянный блок, словарь или деревянный брус, порядок предложений изменится. Так или иначе, появляется другое моментальное решение! (См. решения к упражнениям в конце этой главы.)
То, что «латеральный» метод не приходит на ум первым, объясняется, вероятно, его вдвойне парадоксальной натурой. Познания в области математики и начальственные привычки оказываются препятствиями. Решение находится вне проблемы. Соблазнительно щегольнуть своими знаниями, и потом, когда вопрос поставлен, зачем ходить куда-то еще, если ответ под рукой? В конце концов, ошибка учета корректируется в бухгалтерии, а чтобы устранить неполадки в моторе, нужно чинить сам мотор, правильно? Оказывается, не всегда.
Связь между творчеством и парадоксом изматывает. Возможно, творчество и есть парадокс. Как только удается установить правду, довести до совершенства творческую технику или добиться хороших результатов с помощью нового метода, возникает срочная необходимость доказать, что иногда обратное тоже работает. Тогда вы рискуете покинуть мир творчества и уйти в мир алгоритмов, где от машин ожидается только умение прогнать программу.
Чтобы проиллюстрировать это утверждение, вернемся к нашему упражнению. Мы дублировали систему и создали виртуальную систему-близнеца, где все становилось простым. Вот еще одно небольшое упражнение, которое покажет, что тут нет никакого метода, а есть только творческий подход. Эта задача тоже решается чрезвычайно просто. Только делать все нужно совершенно наоборот! Из двух систем необходимо создать одну.
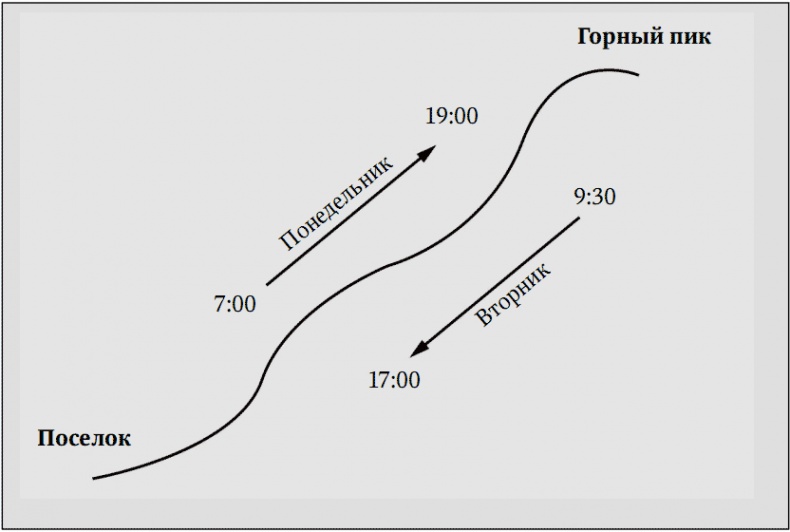
Действие происходит в Альпах. Опытная альпинистка решает взойти на гору, которую ей раньше никогда не удавалось покорить. Существует только одна тропа, но она очень извилиста. Некоторые ее отрезки достаточно просты, и их можно преодолеть легко, другие намного круче, и подъем идет гораздо медленнее. Восхождение, считая все остановки и перерывы, длится 12 часов. Уйдя в 7 часов утра, альпинистка доходит до стоянки в 7 вечера. Отдохнув ночью, она решает вернуться в поселок.
Это гораздо менее утомительно, и просто из интереса она решает спуститься без остановок. Уйдя в 9:30 утра, она приходит к подножию горы в 5 вечера. Внимание, вопрос: есть ли точка на тропе, через которую альпинистка проходит в одно и то же время во время подъема и на пути назад?
Это непросто! Скорости различны, привалы происходили в разное время, и спуск короче, чем подъем. (Решение – в конце главы.)
Я недаром сопоставил эти два упражнения. Творчество нельзя описать формулой. Один подход может годиться для некоей ситуации, а в другой будет лучше работать противоположный ему.
Следующая сцена разворачивается в суде. Судья предлагает сторонам в процессе представить свою версию конфликта. Истец описывает факты только частично, доказывая, что его оппонент был неправ.
– Я прекрасно вас понимаю, – говорит судья. – Вы совершенно правы.
– Что? – возмущается ответчик. – Я еще не успел ничего сказать, а вы уже говорите моему оппоненту, что он прав?
Ответчик пункт за пунктом опровергает все обвинения, доказывая, что это он был прав во всех отношениях.
– Я согласен, – говорит судья. – Если все было так, я полностью на вашей стороне. Вы совершенно правы.
Тут до плеча судьи дотрагивается судебный клерк и говорит, что обе стороны не могут быть правы одновременно.
– Вы совершенно правы, – соглашается судья.
Решения упражнений
1. Еще один хороший пример дошел до нас от несравненного Исаака Ньютона. Развитие его бинома (х + а)n, который является для алгебры тем, чем бетховенская Девятая симфония для музыки, дает нам немедленный ответ, когда мы задаем х = а = 1.
2. 79! Для этого необходимо увидеть, что ответ заложен в самом вопросе! Если вы посмотрите на теннисный турнир сквозь призму «латерального мышления», то увидите, что цель каждого матча состоит в том, чтобы исключить одного из игроков. Тогда, если в итоге должны выбыть все игроки, кроме одного, то количество сыгранных матчей будет равно количеству игроков минус один! Это тот случай, когда время, необходимое для того, чтобы просчитать решение, не зависит от размеров задачи.
3. Достаточно поставить коробку на угол стола и опустить ее вниз на расстояние, равное ее ширине. Таким образом, вы создаете пространство, идентичное размерам коробки. А затем уже вы производите нужные измерения в этом пространстве. Слишком просто, чтобы быть очевидным? И да, и нет. Однажды один ребенок предложил опустить коробку в грязь.
4. Если тут возникают проблемы, они коренятся в нежелании выслушать сам вопрос. Рассудок начинает размышлять, где это место, и есть ли оно вообще. Давайте объединим две системы в одну. Представьте, что два дня совмещаются, как две фотографии на фотоаппарате, на котором мы забыли перемотать пленку. Что происходит? Нечто очень простое: все указывает на то, что две альпинистки (понедельничная и вторничная) пройдут друг мимо друга, и в этот момент они будут находиться в одном месте и, естественно, в одно время. Ответ на заданный вопрос, следовательно: да, конечно!
Глава 6
Магия воображения
Когда не понимаете, что происходит, сделайте вид, что это вы все устроили.
Жан Кокто
Почему начинает бить волшебный фонтан идей? Что за магия стоит за силой воображения?
В XIX веке многие задавались вопросом, бывает ли, что все четыре копыта лошади, несущейся галопом, оказываются в воздухе, или же одно копыто всегда касается земли? Ответа на этот вопрос не было до 1872 года, пока железнодорожный магнат Лиланд Стэнфорд, заключив пари, не нанял фотографа Эдварда Майбриджа, который запечатлел лошадь на полном скаку. Когда серию фотографий проявили, мир получил ответ: все четыре копыта парили над землей.
С мышлением то же самое. Можно представить обыденные мысли, которые носятся у нас в голове, но воображение скорее похоже на галопирующего скакуна, от которого обычные мысли разбегаются в разные стороны. Но на самом деле штука не только в этом. Разнообразные прорывы, совершенные в так называемых науках о мышлении, позволяют отчасти изучить процесс рождения новой идеи, процесс, который мы называем мыслью. Между моментом, когда идеи нет, и моментом, когда она есть, не перекинут мост, даже простенький настил не уложен. Есть лишь несколько четких шагов.

